More Regression

Kelly McConville

Stat 100
Week 7 | Fall 2023

Announcements

Don’t forget about this week’s lecture quiz.

Goals for Today

Handling categorical, explanatory variables with more than 2 categories

Regression with polynomial explanatory variables

But first, does everyone have their randomly generated number?

Then let’s do a quick survey.

Go to bit.ly/stat-100-pumpkin

Linear Regression

Model Form:

\[ \begin{align} y &= \beta_o + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \epsilon \end{align} \]

Linear regression is a flexible class of models that allow for:

Both quantitative and categorical explanatory variables.
Multiple explanatory variables.
Curved relationships between the response variable and the explanatory variable.
BUT the response variable is quantitative.

Example: Movies

Let’s model a movie’s critic rating using the audience rating and the movie’s genre.

library(tidyverse)
movies <- read_csv("https://www.lock5stat.com/datasets2e/HollywoodMovies.csv")

# Restrict our attention to dramas, horrors, and actions
movies2 <- movies %>%
  filter(Genre %in% c("Drama", "Horror", "Action")) %>%
  drop_na(Genre, AudienceScore, RottenTomatoes)
glimpse(movies2)

Rows: 313
Columns: 16
$ Movie            <chr> "Spider-Man 3", "Transformers", "Pirates of the Carib…
$ LeadStudio       <chr> "Sony", "Paramount", "Disney", "Warner Bros", "Warner…
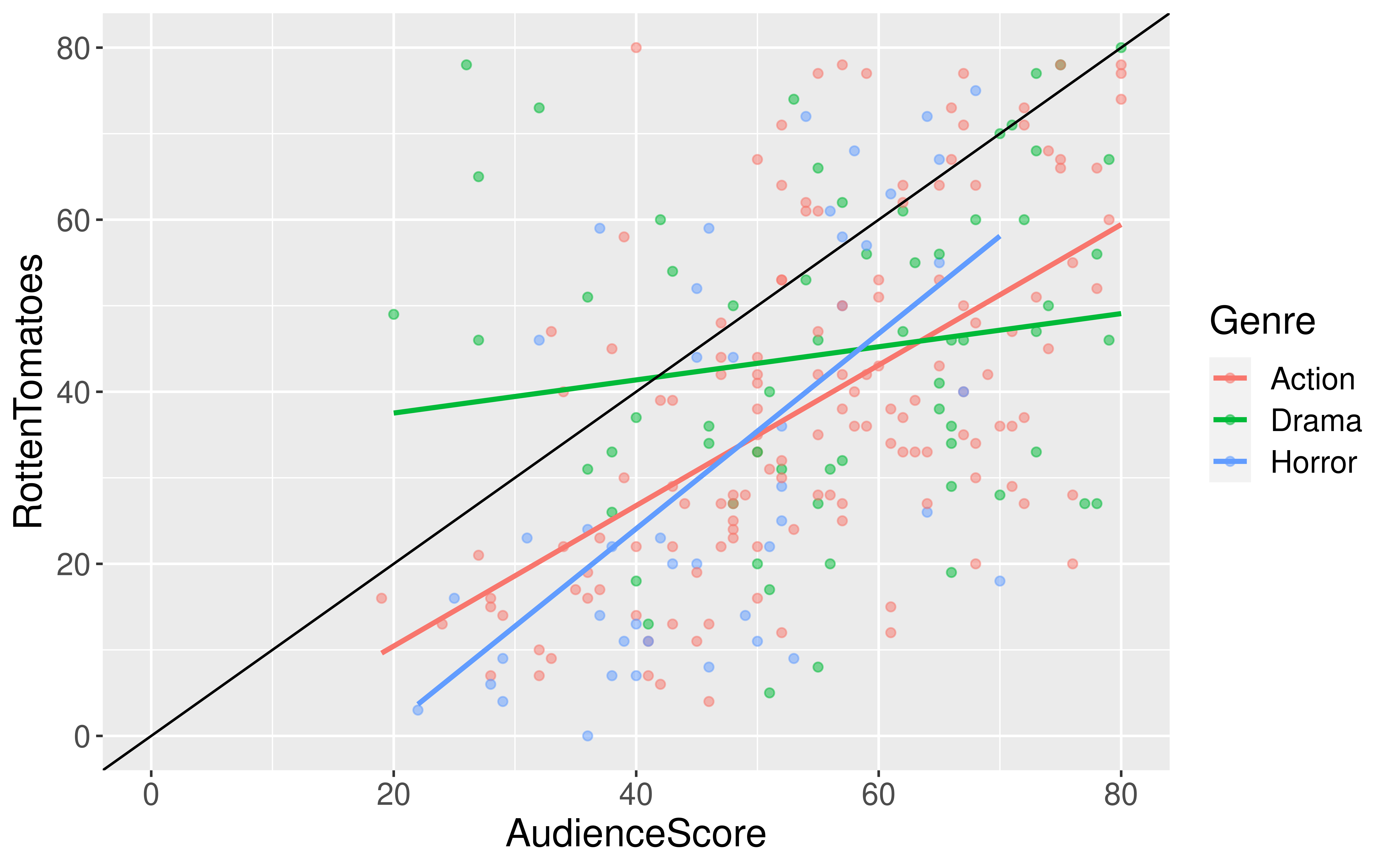
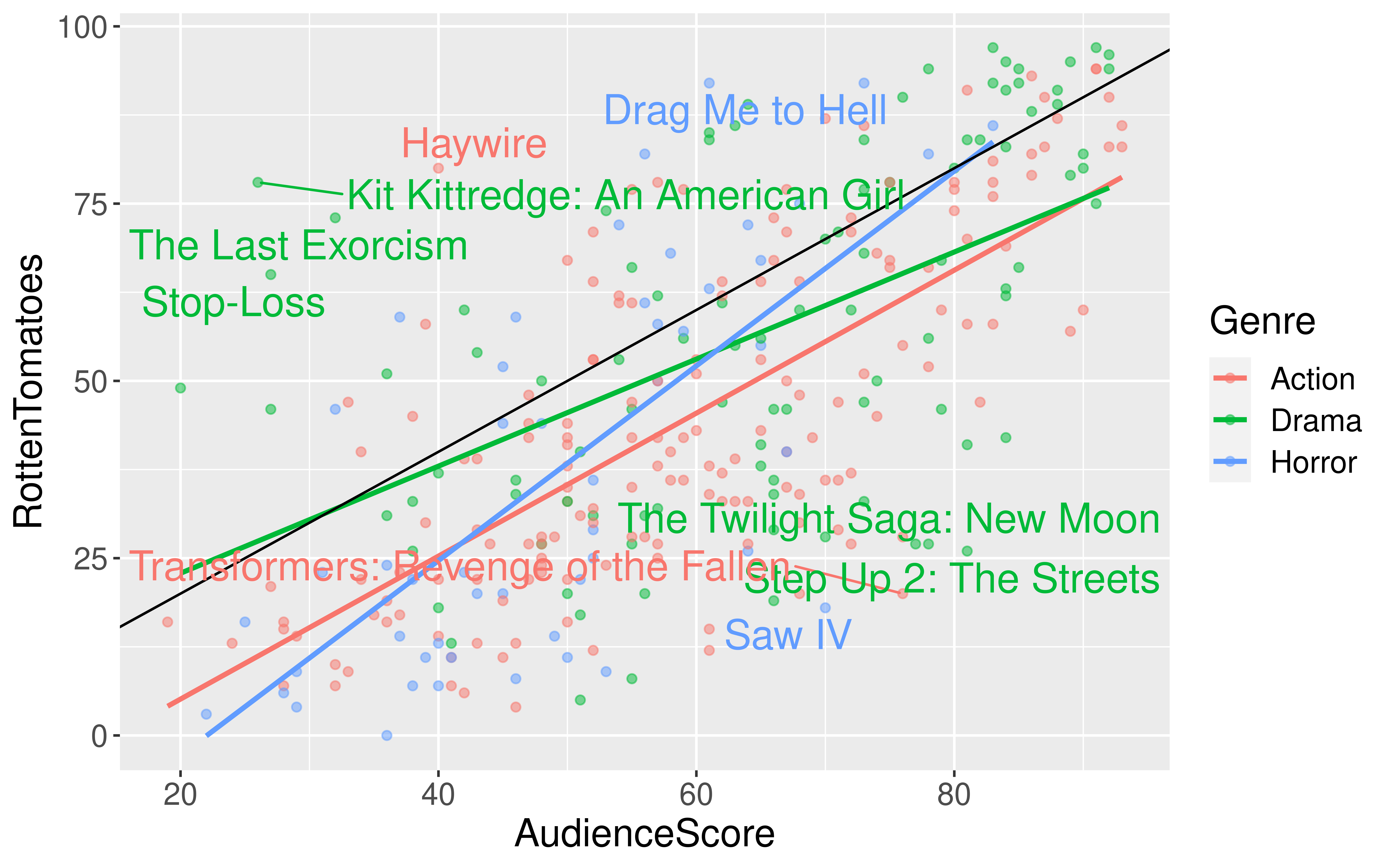
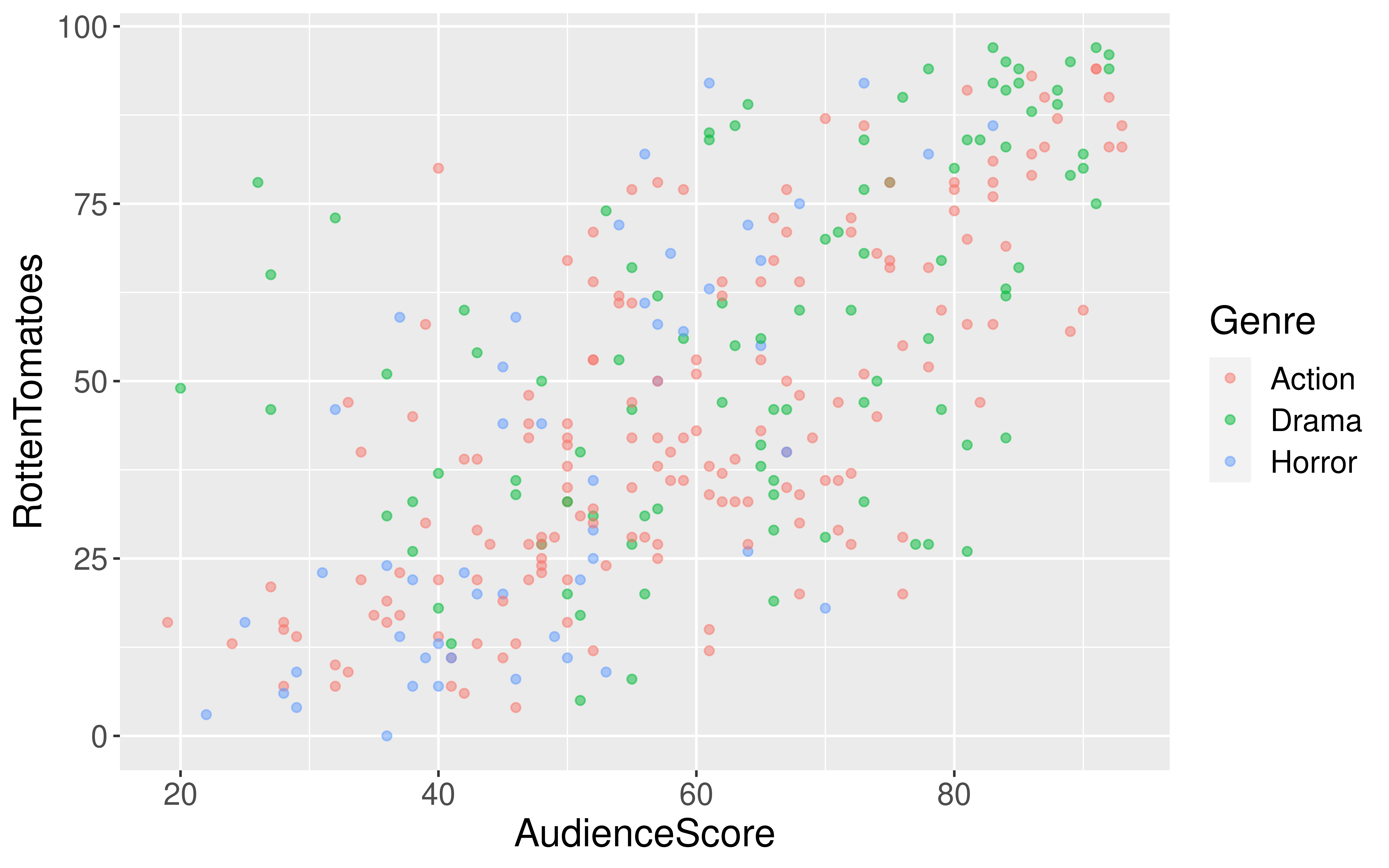
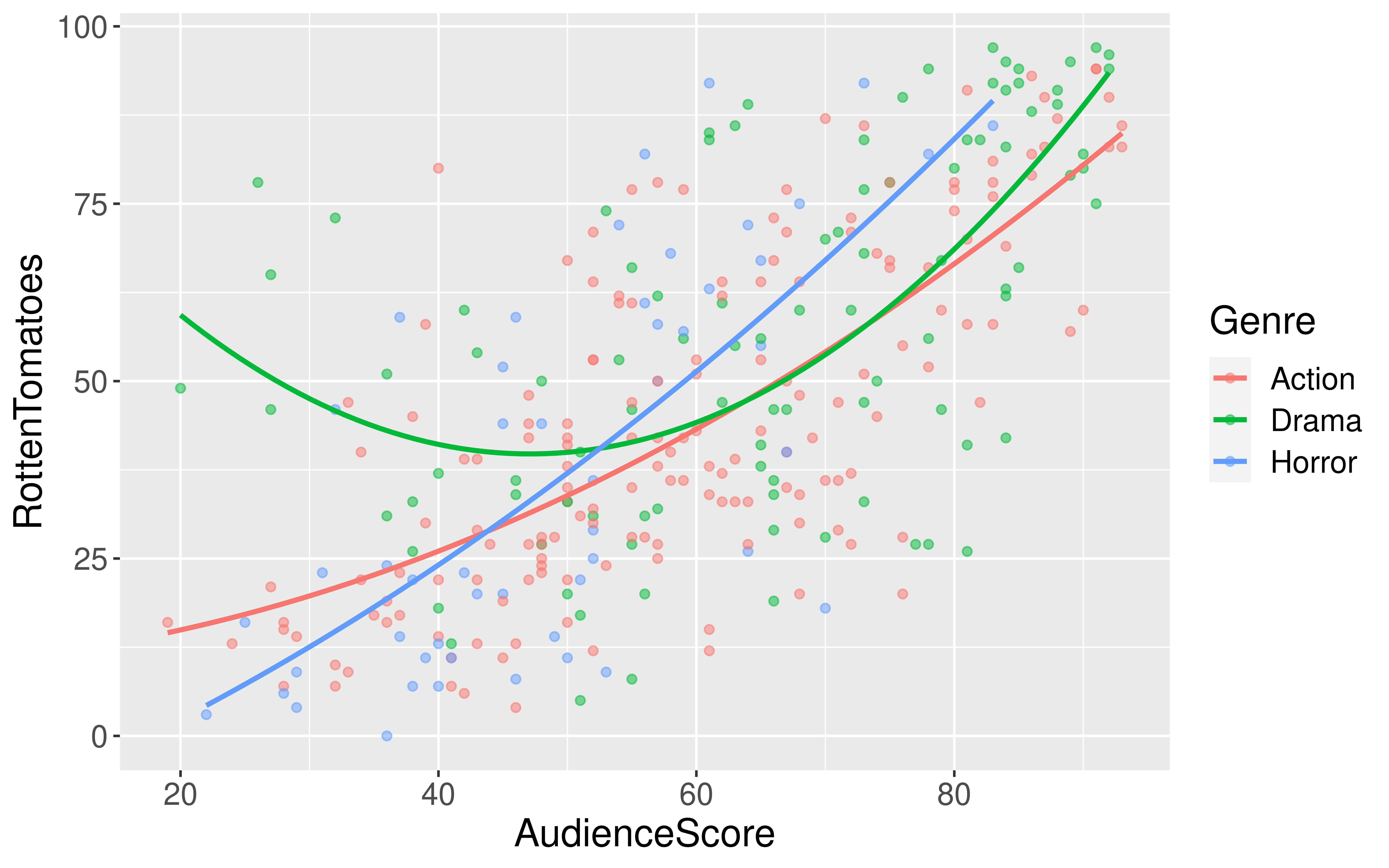
$ RottenTomatoes   <dbl> 61, 57, 45, 60, 20, 79, 35, 28, 41, 71, 95, 42, 18, 2…
$ AudienceScore    <dbl> 54, 89, 74, 90, 68, 86, 55, 56, 81, 52, 84, 55, 70, 6…
$ Story            <chr> "Metamorphosis", "Monster Force", "Rescue", "Sacrific…
$ Genre            <chr> "Action", "Action", "Action", "Action", "Action", "Ac…
$ TheatersOpenWeek <dbl> 4252, 4011, 4362, 3103, 3778, 3408, 3959, 3619, 2911,…
$ OpeningWeekend   <dbl> 151.1, 70.5, 114.7, 70.9, 49.1, 33.4, 58.0, 45.3, 19.…
$ BOAvgOpenWeekend <dbl> 35540, 17577, 26302, 22844, 12996, 9791, 14663, 12541…
$ DomesticGross    <dbl> 336.53, 319.25, 309.42, 210.61, 140.13, 134.53, 131.9…
$ ForeignGross     <dbl> 554.34, 390.46, 654.00, 245.45, 117.90, 249.00, 157.1…
$ WorldGross       <dbl> 890.87, 709.71, 963.42, 456.07, 258.02, 383.53, 289.0…
$ Budget           <dbl> 258.0, 150.0, 300.0, 65.0, 140.0, 110.0, 130.0, 110.0…
$ Profitability    <dbl> 345.30, 473.14, 321.14, 701.64, 184.30, 348.66, 222.3…
$ OpenProfit       <dbl> 58.57, 47.00, 38.23, 109.08, 35.07, 30.36, 44.62, 41.…
$ Year             <dbl> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007,…

Response variable:

Explanatory variables:

How should we encode a categorical variable with more than 2 categories?

Let’s start with what NOT to do.

Equal Slopes Model:

How should we encode a categorical variable with more than 2 categories?

What we should do instead.

Equal Slopes Model:

How should we encode a categorical variable with more than 2 categories?

Different Slopes Model:

Exploring the Data

ggplot(data = movies2,
       mapping = aes(x = AudienceScore,
                     y = RottenTomatoes,
                     color = Genre)) +
  geom_point(alpha = 0.5) +
  stat_smooth(method = lm, se = FALSE) +
  geom_abline(slope = 1, intercept = 0) +
  xlim(0, 80) + ylim(0, 80)

Trends?
Should we include interaction terms in the model?

outliers <- movies2 %>%
  mutate(DiffScore = AudienceScore - RottenTomatoes) %>%
  filter(DiffScore > 50 | DiffScore < -30) %>%
  select(Movie, DiffScore, AudienceScore, RottenTomatoes, Genre)
outliers

# A tibble: 9 × 5
  Movie                             DiffScore AudienceScore RottenTomatoes Genre
  <chr>                                 <dbl>         <dbl>          <dbl> <chr>
1 Saw IV                                   52            70             18 Horr…
2 Step Up 2: The Streets                   55            81             26 Drama
3 Kit Kittredge: An American Girl         -52            26             78 Drama
4 Stop-Loss                               -38            27             65 Drama
5 Transformers: Revenge of the Fal…        56            76             20 Acti…
6 The Twilight Saga: New Moon              51            78             27 Drama
7 Drag Me to Hell                         -31            61             92 Horr…
8 The Last Exorcism                       -41            32             73 Drama
9 Haywire                                 -40            40             80 Acti…

library(ggrepel)
ggplot(data = movies2,
       mapping = aes(x = AudienceScore,
                     y = RottenTomatoes,
                     color = Genre)) +
  geom_point(alpha = 0.5) +
  stat_smooth(method = lm, se = FALSE) +
  geom_abline(slope = 1, intercept = 0) +
  geom_text_repel(data = outliers,
                  mapping = aes(label =
                                  Movie),
                  force = 10,
                  show.legend = FALSE,
                  size = 6)

Building the Model:

Full model form:

mod <- lm(RottenTomatoes ~ AudienceScore*Genre, data = movies2)

library(moderndive)
get_regression_table(mod)

# A tibble: 6 × 7
  term                    estimate std_error statistic p_value lower_ci upper_ci
  <chr>                      <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept                -15.0       5.27      -2.85   0.005  -25.4     -4.67 
2 AudienceScore              1.01      0.085     11.8    0        0.84     1.18 
3 Genre: Drama              22.8       8.94       2.55   0.011    5.23    40.4  
4 Genre: Horror            -15.2      11.0       -1.39   0.165  -36.8      6.32 
5 AudienceScore:GenreDra…   -0.253     0.136     -1.86   0.065   -0.522    0.015
6 AudienceScore:GenreHor…    0.365     0.206      1.77   0.078   -0.04     0.771

Estimated model for Dramas:

Coming Back to Our Exploratory Data Analysis

library(ggrepel)
ggplot(data = movies2,
       mapping = aes(x = AudienceScore,
                     y = RottenTomatoes,
                     color = Genre)) +
  geom_point(alpha = 0.5)

Evidence of curvature?

Adding a Curve to your Scatterplot

ggplot(data = movies2,
       mapping = aes(x = AudienceScore,
                     y = RottenTomatoes,
                     color = Genre)) +
  geom_point(alpha = 0.5) +
  stat_smooth(method = lm, se = FALSE, 
        formula = y ~ poly(x, degree = 2))

Fitting the New Model

mod2 <- lm(RottenTomatoes ~ poly(AudienceScore, degree = 2, raw = TRUE)*Genre, 
           data = movies2)
get_regression_table(mod2, print = TRUE)

term	estimate	std_error	statistic	p_value	lower_ci	upper_ci
intercept	9.922	14.851	0.668	0.505	-19.301	39.145
poly(AudienceScore, degree = 2, raw = TRUE)1	0.098	0.515	0.191	0.849	-0.916	1.113
poly(AudienceScore, degree = 2, raw = TRUE)2	0.008	0.004	1.788	0.075	-0.001	0.016
Genre: Drama	88.923	24.538	3.624	0.000	40.638	137.208
Genre: Horror	-23.767	31.054	-0.765	0.445	-84.876	37.342
poly(AudienceScore, degree = 2, raw = TRUE)1:GenreDrama	-2.608	0.840	-3.107	0.002	-4.260	-0.956
poly(AudienceScore, degree = 2, raw = TRUE)2:GenreDrama	0.019	0.007	2.785	0.006	0.006	0.032
poly(AudienceScore, degree = 2, raw = TRUE)1:GenreHorror	0.574	1.223	0.469	0.639	-1.833	2.981
poly(AudienceScore, degree = 2, raw = TRUE)2:GenreHorror	-0.001	0.012	-0.061	0.951	-0.024	0.022

Let’s Practice with the `palmerpenguins`!

Let’s Practice with the `palmerpenguins`!

library(palmerpenguins)
glimpse(penguins)

Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

Let’s Practice with the `palmerpenguins`!

ggplot(data = penguins,
       mapping = aes(x = flipper_length_mm,
                     y = bill_length_mm,
                     color = species)) +
  geom_point(alpha = 0.7) +
  stat_smooth(method = "lm", se = FALSE)

mod1 <- lm(bill_length_mm ~ flipper_length_mm + species, data = penguins)
get_regression_table(mod1)

# A tibble: 4 × 7
  term               estimate std_error statistic p_value lower_ci upper_ci
  <chr>                 <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept            -2.06      4.04      -0.51   0.611  -10.0      5.88 
2 flipper_length_mm     0.215     0.021     10.1    0        0.173    0.257
3 species: Chinstrap    8.78      0.399     22.0    0        8.00     9.56 
4 species: Gentoo       2.86      0.659      4.34   0        1.56     4.15

mod2 <- lm(bill_length_mm ~ flipper_length_mm * species, data = penguins)
get_regression_table(mod2)

# A tibble: 6 × 7
  term                    estimate std_error statistic p_value lower_ci upper_ci
  <chr>                      <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
1 intercept                 13.6       6.05      2.25    0.025    1.68    25.5  
2 flipper_length_mm          0.133     0.032     4.17    0        0.07     0.195
3 species: Chinstrap        -7.99     10.5      -0.763   0.446  -28.6     12.6  
4 species: Gentoo          -34.3       9.82     -3.50    0.001  -53.6    -15.0  
5 flipper_length_mm:spec…    0.088     0.054     1.63    0.104   -0.018    0.194
6 flipper_length_mm:spec…    0.182     0.048     3.80    0        0.088    0.275

Practice

Determine and interpret the slope for a Chinstrap penguin using Model 1.

Determine and interpret the slope for a Adelie penguin using Model 1.

In Model 1, interpret \(\hat{\beta}_2\).

Determine and interpret the slope for a Chinstrap penguin using Model 2.

Determine and interpret the slope for a Adelie penguin using Model 2.

Announcements

Goals for Today

But first, does everyone have their randomly generated number?

Then let’s do a quick survey.

Linear Regression

Example: Movies

How should we encode a categorical variable with more than 2 categories?

How should we encode a categorical variable with more than 2 categories?

How should we encode a categorical variable with more than 2 categories?

Exploring the Data

Side-bar: Identify Outliers on a Graph

Side-bar: Identify Outliers on a Graph

Building the Model:

Coming Back to Our Exploratory Data Analysis

Adding a Curve to your Scatterplot

Fitting the New Model

Let’s Practice with the `palmerpenguins`!

Let’s Practice with the `palmerpenguins`!

Let’s Practice with the `palmerpenguins`!

Practice

Announcements

Goals for Today

But first, does everyone have their randomly generated number?

Then let’s do a quick survey.

Linear Regression

Example: Movies

How should we encode a categorical variable with more than 2 categories?

How should we encode a categorical variable with more than 2 categories?

How should we encode a categorical variable with more than 2 categories?

Exploring the Data

Side-bar: Identify Outliers on a Graph

Side-bar: Identify Outliers on a Graph

Building the Model:

Coming Back to Our Exploratory Data Analysis

Adding a Curve to your Scatterplot

Fitting the New Model

Let’s Practice with the palmerpenguins!

Let’s Practice with the palmerpenguins!

Let’s Practice with the palmerpenguins!

Practice

Let’s Practice with the `palmerpenguins`!

Let’s Practice with the `palmerpenguins`!

Let’s Practice with the `palmerpenguins`!