Sampling Distributions
Kelly McConville
Stat 100
Week 8 | Fall 2023
Announcements
- Oct 30th: Hex or Treat Day in Stat 100
- Wear a Halloween costume and get either a hex sticker or candy!!
Goals for Today
Modeling & Ethics: Algorithmic bias
Sampling Distribution
- Properties
- Construction in
R
- Estimation
Data Ethics: Algorithmic Bias
Return to the Americian Statistical Association’s “Ethical Guidelines for Statistical Practice”
Integrity of Data and Methods
“The ethical statistical practitioner seeks to understand and mitigate known or suspected limitations, defects, or biases in the data or methods and communicates potential impacts on the interpretation, conclusions, recommendations, decisions, or other results of statistical practices.”
“For models and algorithms designed to inform or implement decisions repeatedly, develops and/or implements plans to validate assumptions and assess performance over time, as needed. Considers criteria and mitigation plans for model or algorithm failure and retirement.”
Algorithmic Bias
Algorithmic bias: when the model systematically creates unfair outcomes, such as privileging one group over another.
Example: The Coded Gaze
Facial recognition software struggles to see faces of color.
Algorithms built on a non-diverse, biased dataset.
Algorithmic Bias
Algorithmic bias: when the model systematically creates unfair outcomes, such as privileging one group over another.
Example: COMPAS model used throughout the country to predict recidivism
- Differences in predictions across race and gender

- Cynthia Rudin and collaborators wrote The Age of Secrecy and Unfairness in Recidivism Prediction
- Argue for the need for transparency in models that make such important decisions.
Sampling Distribution of a Statistic
Steps to Construct an (Approximate) Sampling Distribution:
Decide on a sample size, \(n\).
Randomly select a sample of size \(n\) from the population.
Compute the sample statistic.
Put the sample back in.
Repeat Steps 2 - 4 many (1000+) times.
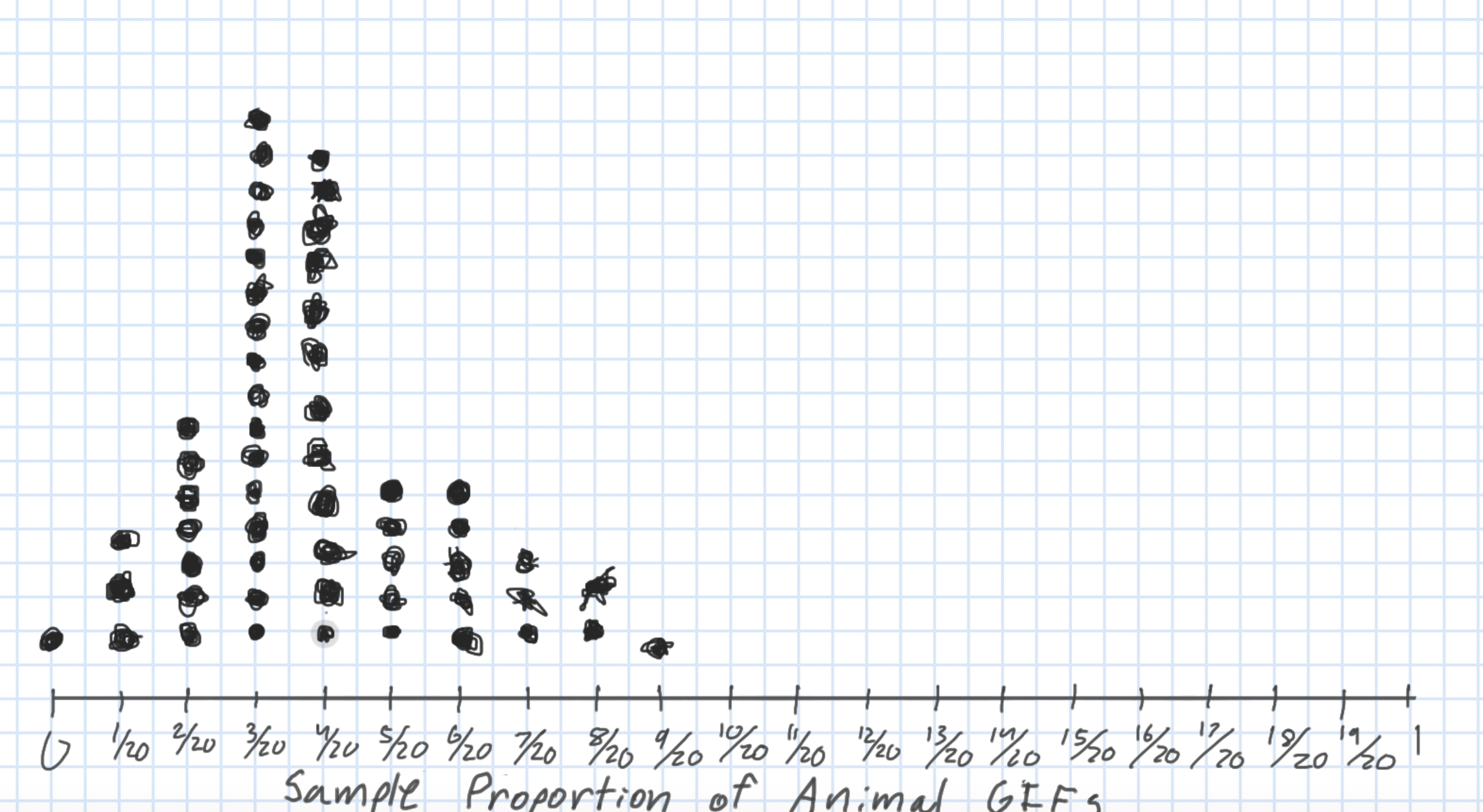
What happens to the center/spread/shape as we increase the sample size?
What happens to the center/spread/shape if the true parameter changes?
Let’s Construct Some Sampling Distributions using R!
Important Notes
To construct a sampling distribution for a statistic, we need access to the entire population so that we can take repeated samples from the population.
- Population = Harvard trees
But if we have access to the entire population, then we know the value of the population parameter.
- Can compute the exact mean diameter of trees in our population.
The sampling distribution is needed in the exact scenario where we can’t compute it: the scenario where we only have a single sample.
We will learn how to estimate the sampling distribution soon.
Today, we have the entire population and are constructing sampling distributions anyway to study their properties!
New R Package: infer
- Will use
inferto conduct statistical inference.
Our Population Parameter
Create data frame of Harvard trees:
Add variable of interest:
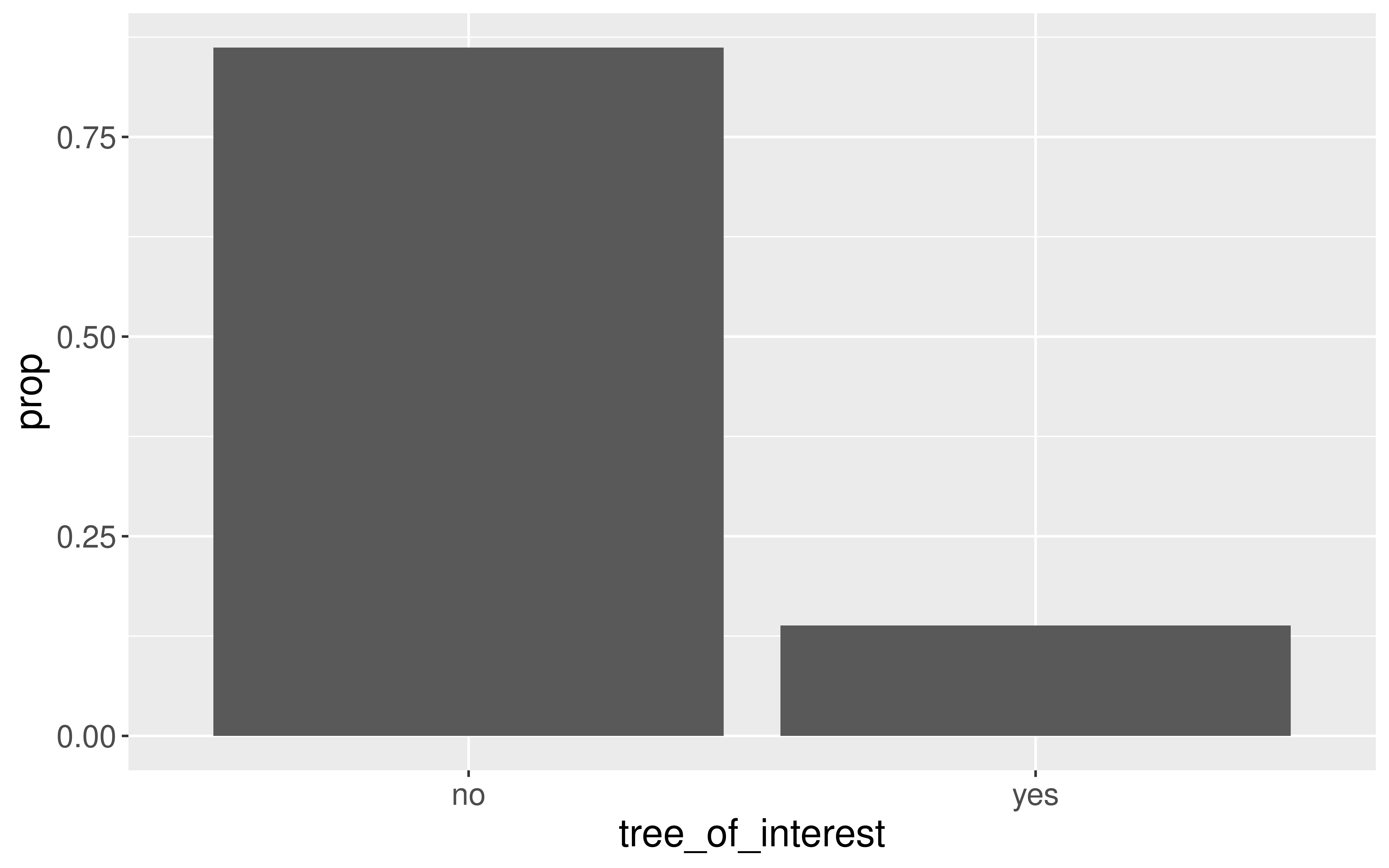
Population Parameter
Random Samples
Let’s look at 4 random samples.
Constructing the Sampling Distribution
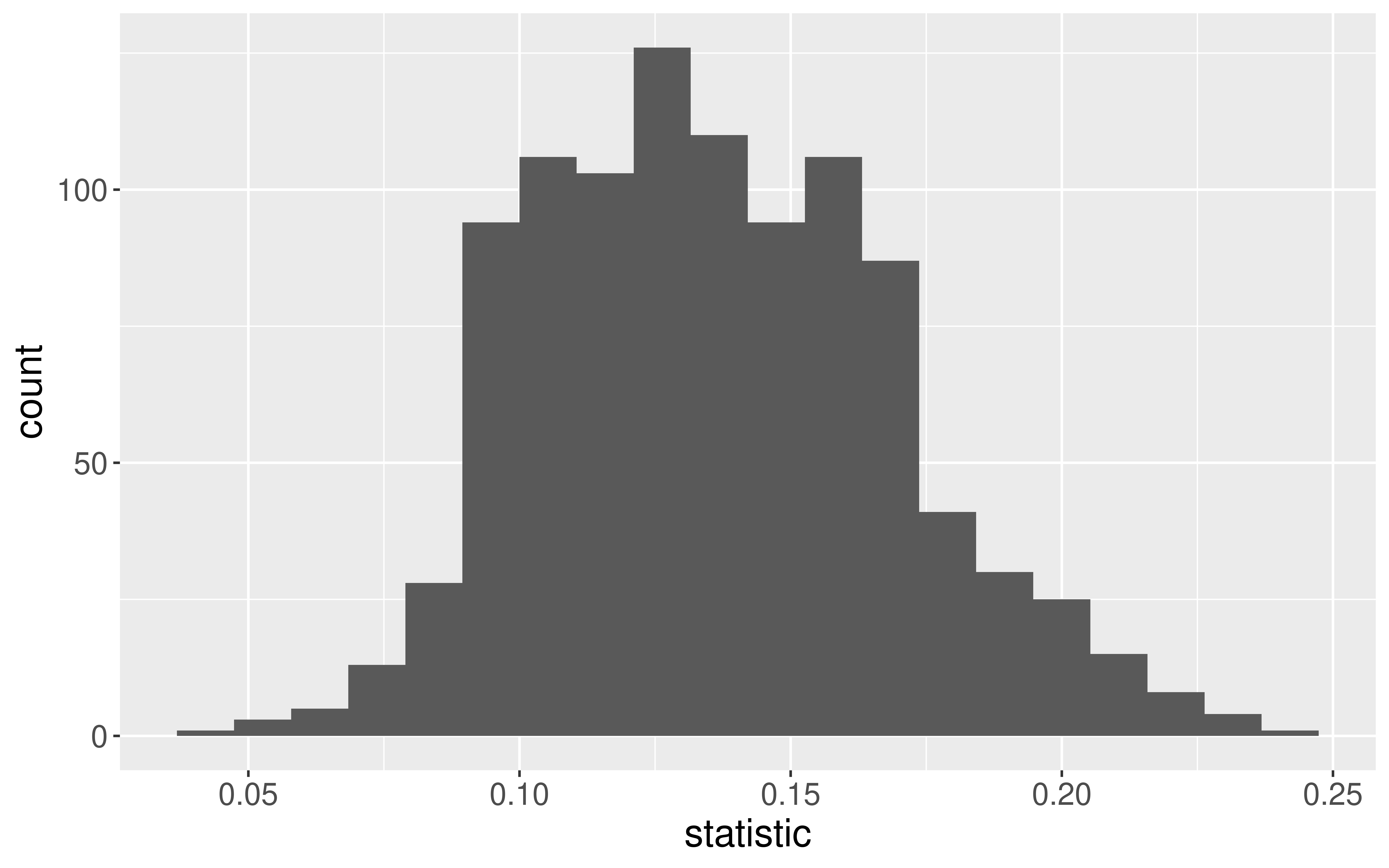
Now, let’s take 1000 random samples.
# Construct the sampling distribution
samp_dist <- harTrees %>%
rep_sample_n(size = 20, reps = 1000) %>%
group_by(replicate) %>%
summarize(statistic =
mean(tree_of_interest == "yes"))
# Graph the sampling distribution
ggplot(data = samp_dist,
mapping = aes(x = statistic)) +
geom_histogram(bins = 14)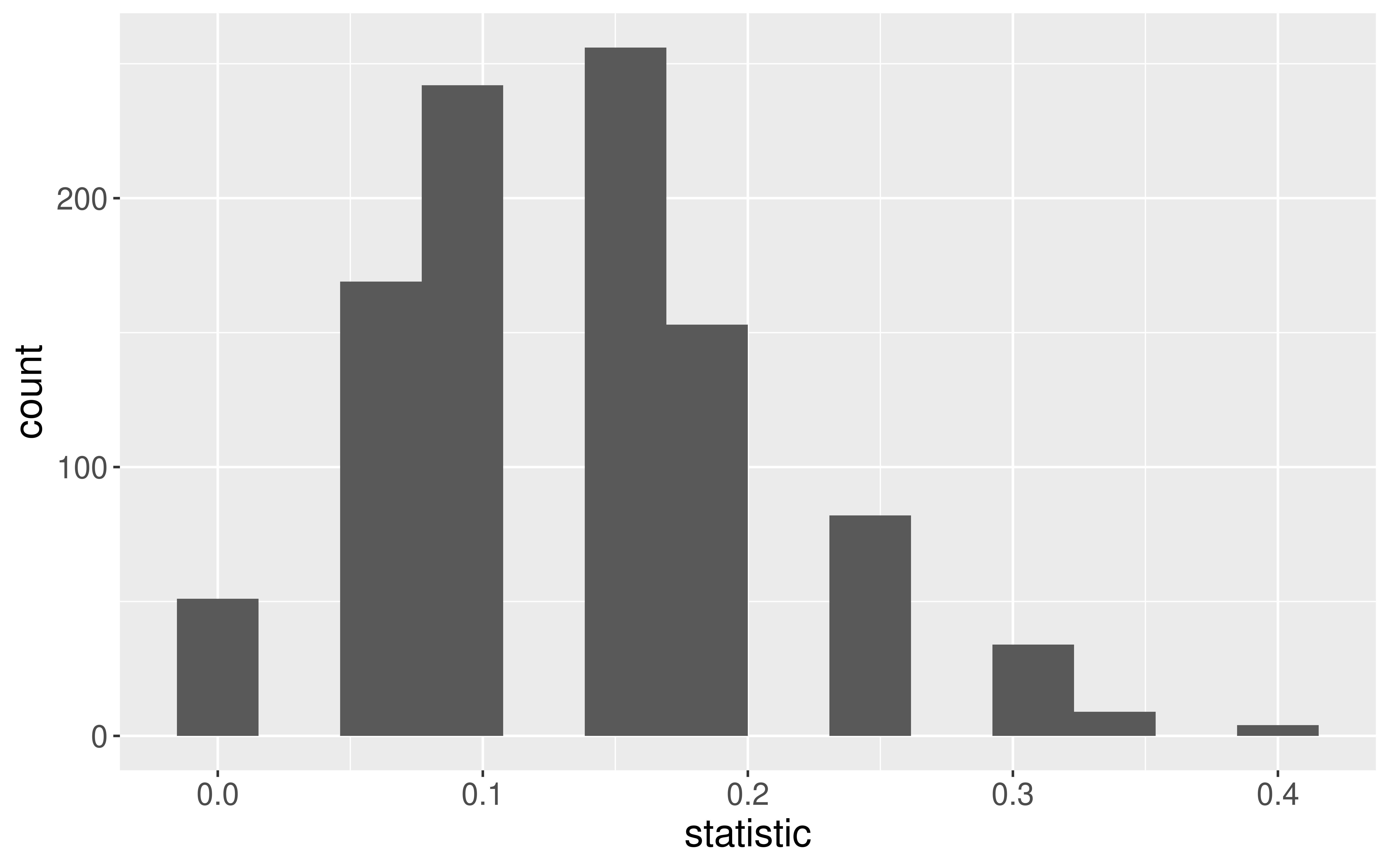
- Shape?
- Center?
- Spread?
Properties of the Sampling Distribution
The standard deviation of a sample statistic is called the standard error.
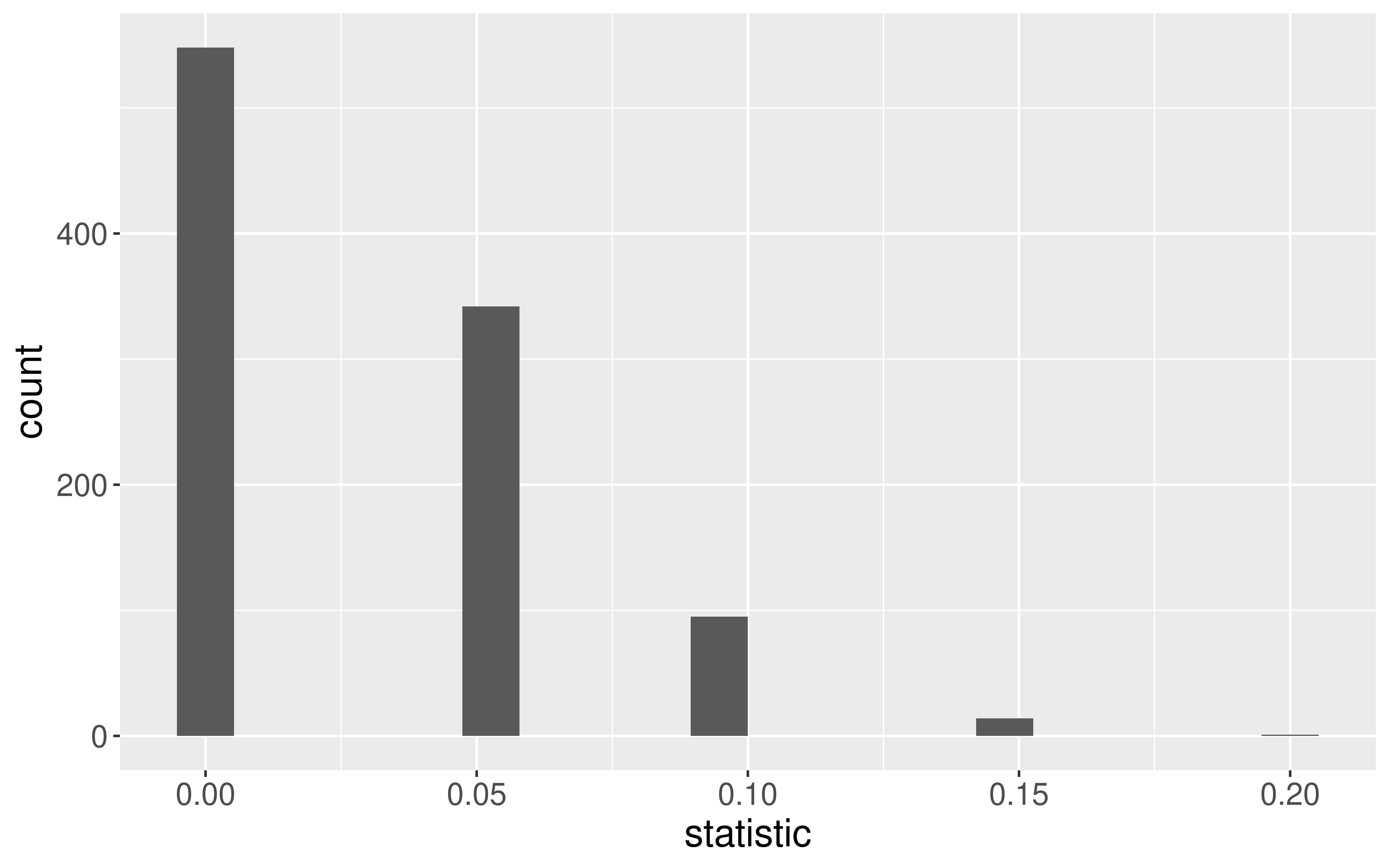
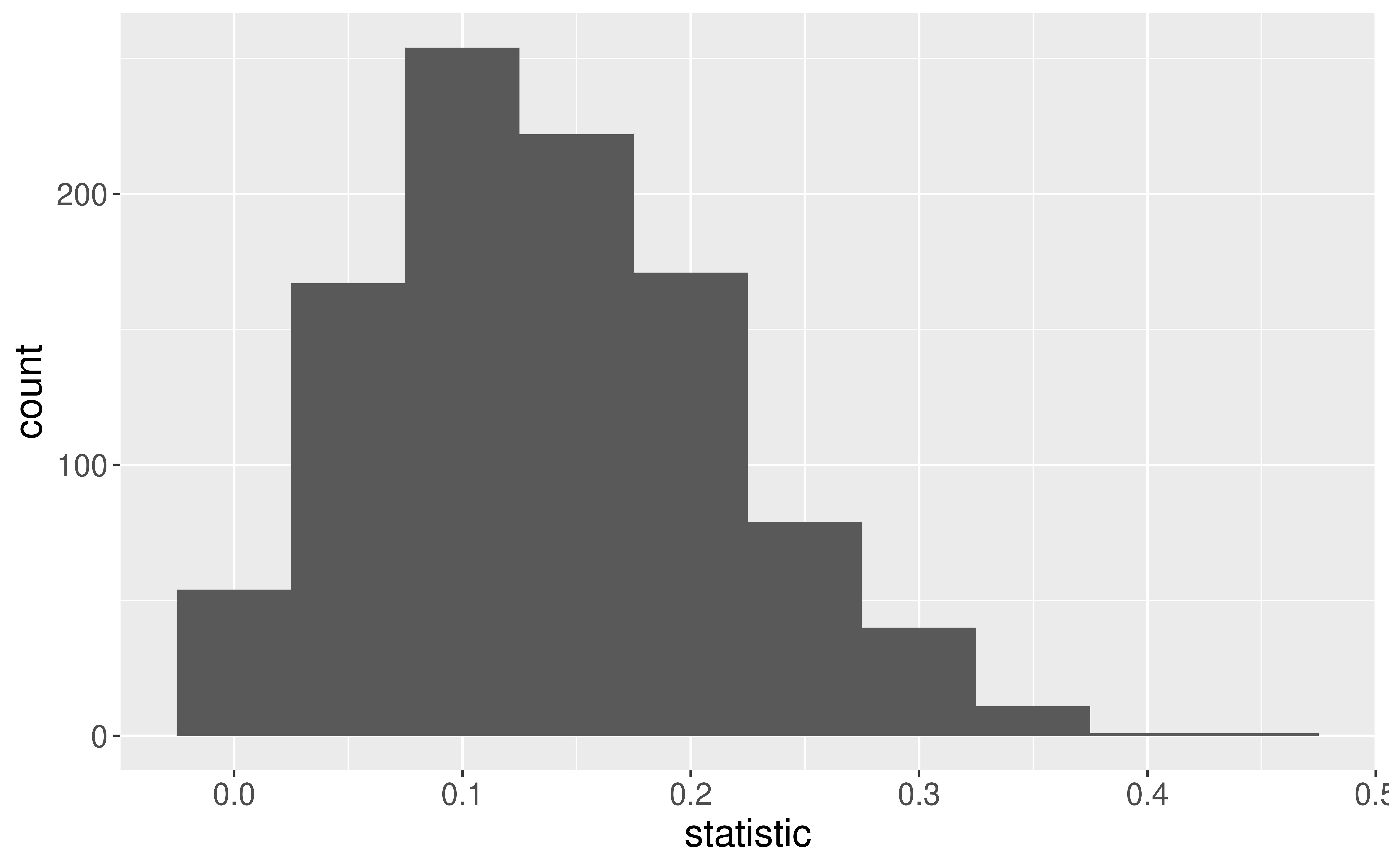
What happens to the sampling distribution if we change the sample size from 20 to 100?
# Construct the sampling distribution
samp_dist <- harTrees %>%
rep_sample_n(size = 100, reps = 1000) %>%
group_by(replicate) %>%
summarize(statistic =
mean(tree_of_interest == "yes"))
# Graph the sampling distribution
ggplot(data = samp_dist,
mapping = aes(x = statistic)) +
geom_histogram(bins = 20)What if we change the true parameter value?
On P-Set 5, will investigate what happens when we change the parameter of interest to a mean or a correlation coefficient!
Key Features of a Sampling Distribution
What did we learn about sampling distributions?
Centered around the true population parameter.
As the sample size increases, the standard error (SE) of the statistic decreases.
As the sample size increases, the shape of the sampling distribution becomes more bell-shaped and symmetric.
Question: How do sampling distributions help us quantify uncertainty?
Question: If I am estimating a parameter in a real example, why won’t I be able to construct the sampling distribution??
Estimation
Goal: Estimate the value of a population parameter using data from the sample.
Question: How do I know which population parameter I am interesting in estimating?
Answer: Likely depends on the research question and structure of your data!
Point Estimate: The corresponding statistic
- Single best guess for the parameter
Potential Parameters and Point Estimates
Confidence Intervals
It is time to move beyond just point estimates to interval estimates that quantify our uncertainty.
Confidence Interval: Interval of plausible values for a parameter
Form: \(\mbox{statistic} \pm \mbox{Margin of Error}\)
Question: How do we find the Margin of Error (ME)?
Answer: If the sampling distribution of the statistic is approximately bell-shaped and symmetric, then a statistic will be within 2 SEs of the parameter for 95% of the samples.
Form: \(\mbox{statistic} \pm 2\mbox{SE}\)
Called a 95% confidence interval (CI). (Will discuss the meaning of confidence soon)
Confidence Intervals
95% CI Form:
\[ \mbox{statistic} \pm 2\mbox{SE} \]
Let’s use the ce data to produce a CI for the average household income before taxes.
What else do we need to construct the CI?
Problem: To compute the SE, we need many samples from the population. We have 1 sample.
Solution: Approximate the sampling distribution using ONLY OUR ONE SAMPLE!
Reminders:
- Oct 30th: Hex or Treat Day in Stat 100
- Wear a Halloween costume and get either a hex sticker or candy!!