Grab 30 notecards! It is okay if they already have markings on them. And, please return the notecards to the same spot after class.

Confidence Intervals




Kelly McConville

Stat 100
Week 9 | Fall 2023

Announcements

  • Oct 30th Today: Hex or Treat Day in Stat 100
    • If you are wearing a Halloween costume, come to the front before or after class for your hex sticker or treat!

Goals for Today

  • Estimation
  • Bootstrap distributions
  • Bootstrapped confidence intervals

Question: How do sampling distributions help us quantify uncertainty?

Estimation

Goal: Estimate the value of a population parameter using data from the sample.

Sub-Goal: Quantify our uncertainty in using the sample to say something about the population.

Confidence Interval (CI): Interval of plausible values for a parameter

Form of a 95% Confidence Interval:

\[\begin{align*} \mbox{statistic} &\pm \mbox{Margin of Error}\\ \mbox{statistic} &\pm 2\mbox{SE} \end{align*}\]

Problem: To compute the SE, we need many samples from the population. We have 1 sample.

Solution: Approximate the sampling distribution using ONLY OUR ONE SAMPLE!

Bootstrap Distribution

How do we approximate the sampling distribution?

Bootstrap Distribution of a Sample Statistic:

  1. Take a sample of size \(n\) with replacement from the sample. Called a bootstrap sample.

  2. Compute the statistic on the bootstrap sample.

  3. Repeat 1 and 2 many (1000+) times.

Let’s Practice Generating Bootstrap Samples!

Example: In a recent study, 23 rats showed compassion that surprised scientists. Twenty-three of the 30 rats in the study freed another trapped rat in their cage, even when chocolate served as a distraction and even when the rats would then have to share the chocolate with their freed companion. (Rats, it turns out, love chocolate.) Rats did not open the cage when it was empty or when there was a stuffed animal inside, only when a fellow rat was trapped. We wish to use the sample to estimate the proportion of rats that show empathy in this way.

Parameter:

Statistic:

Use your 30 cards to take a bootstrap sample. (Make sure to appropriately label them first!)

Compute the bootstrap statistic and put it on the class dotplot.

(Will use these data for one of the problems in the next p-set.)

Sampling Distribution Versus Bootstrap Distribution

  • Data needed:




  • Center:




  • Spread:

(Bootstrapped) Confidence Intervals

95% CI Form:

\[ \mbox{statistic} \pm 2\mbox{SE} \]

We approximate \(\mbox{SE}\) with \(\widehat{\mbox{SE}}\) = the standard deviation of the bootstrapped statistics.

Caveats:

  • Assuming a random sample

  • Even with random samples, sometimes we get non-representative samples. Bootstrapping can’t fix that.

  • Assuming the bootstrap distribution is bell-shaped and symmetric

Bootstrapped Confidence Intervals

Two Methods

Assuming random sample and roughly bell-shaped and symmetric bootstrap distribution for both methods.

SE Method 95% CI:

\[ \mbox{statistic} \pm 2\widehat{\mbox{SE}} \]

We approximate \(\mbox{SE}\) with \(\widehat{\mbox{SE}}\) = the standard deviation of the bootstrapped statistics.

Percentile Method CI:

If I want a P% confidence interval, I find the bounds of the middle P% of the bootstrap distribution.

How can we construct bootstrap distributions and bootstrapped CIs in R?

Load Packages and Data

library(tidyverse)
library(infer)

Let’s return to the movies dataset and estimate numerical quantities about Hollywood movies.

# Read in data
movies <- read_csv("https://www.lock5stat.com/datasets2e/HollywoodMovies.csv")

Estimation for a Single Mean

What is the average amount of money \((\mu)\) made in the opening weekend?

# Compute the summary statistic
x_bar <- movies %>%
  drop_na(OpeningWeekend) %>%
  specify(response = OpeningWeekend) %>%
  calculate(stat = "mean")
x_bar
Response: OpeningWeekend (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  20.6
  • Why is our numerical quantity a mean and not a proportion or correlation here?

Estimation for a Single Mean

set.seed(999)


# Construct bootstrap distribution
bootstrap_dist <- movies %>%
  drop_na(OpeningWeekend) %>%
  specify(response = OpeningWeekend) %>%
  generate(reps =  1000, type = "bootstrap") %>%
  calculate(stat = "mean")

# Look at bootstrap distribution
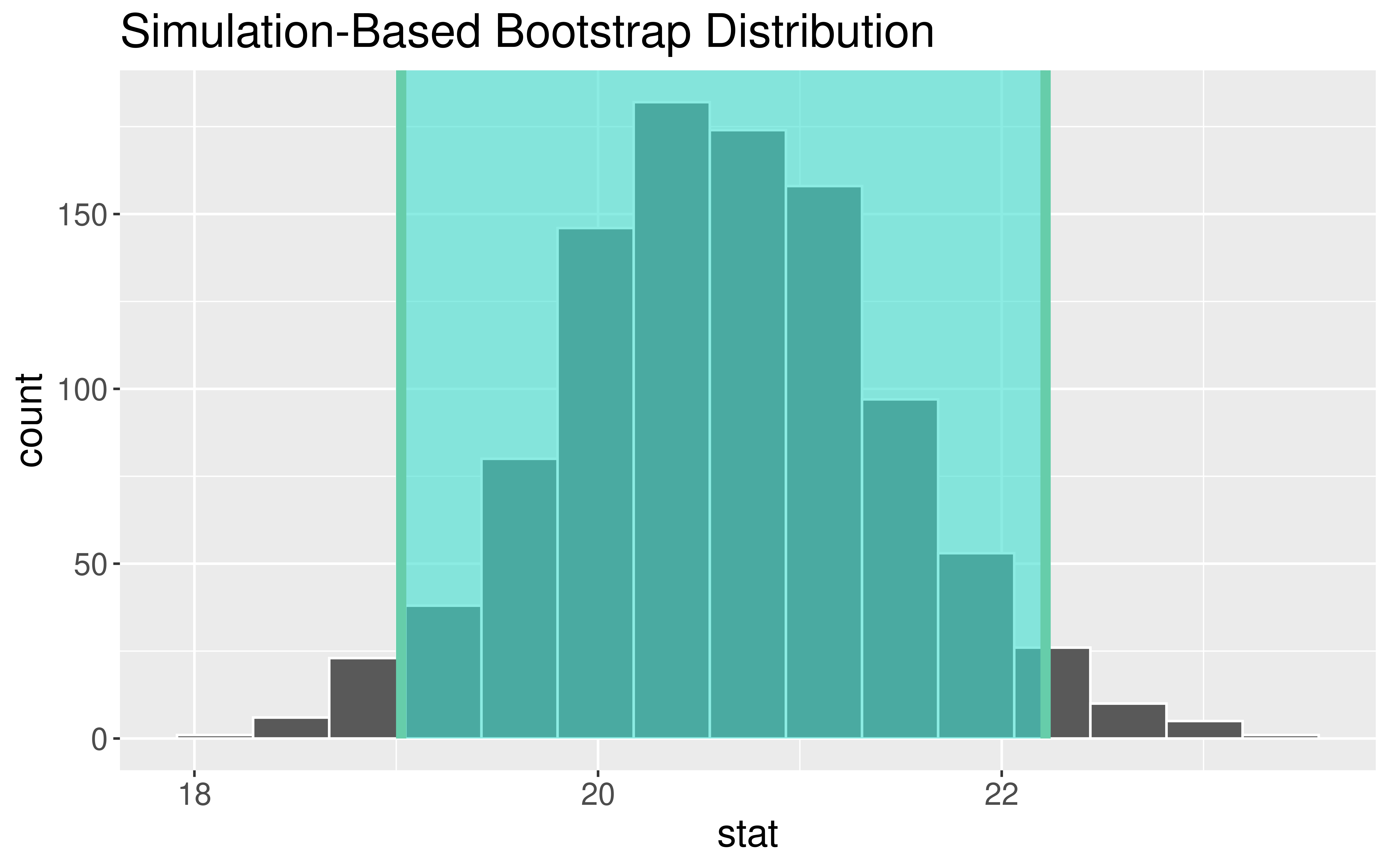
ggplot(data = bootstrap_dist, 
       mapping = aes(x = stat)) +
  geom_histogram(color = "white")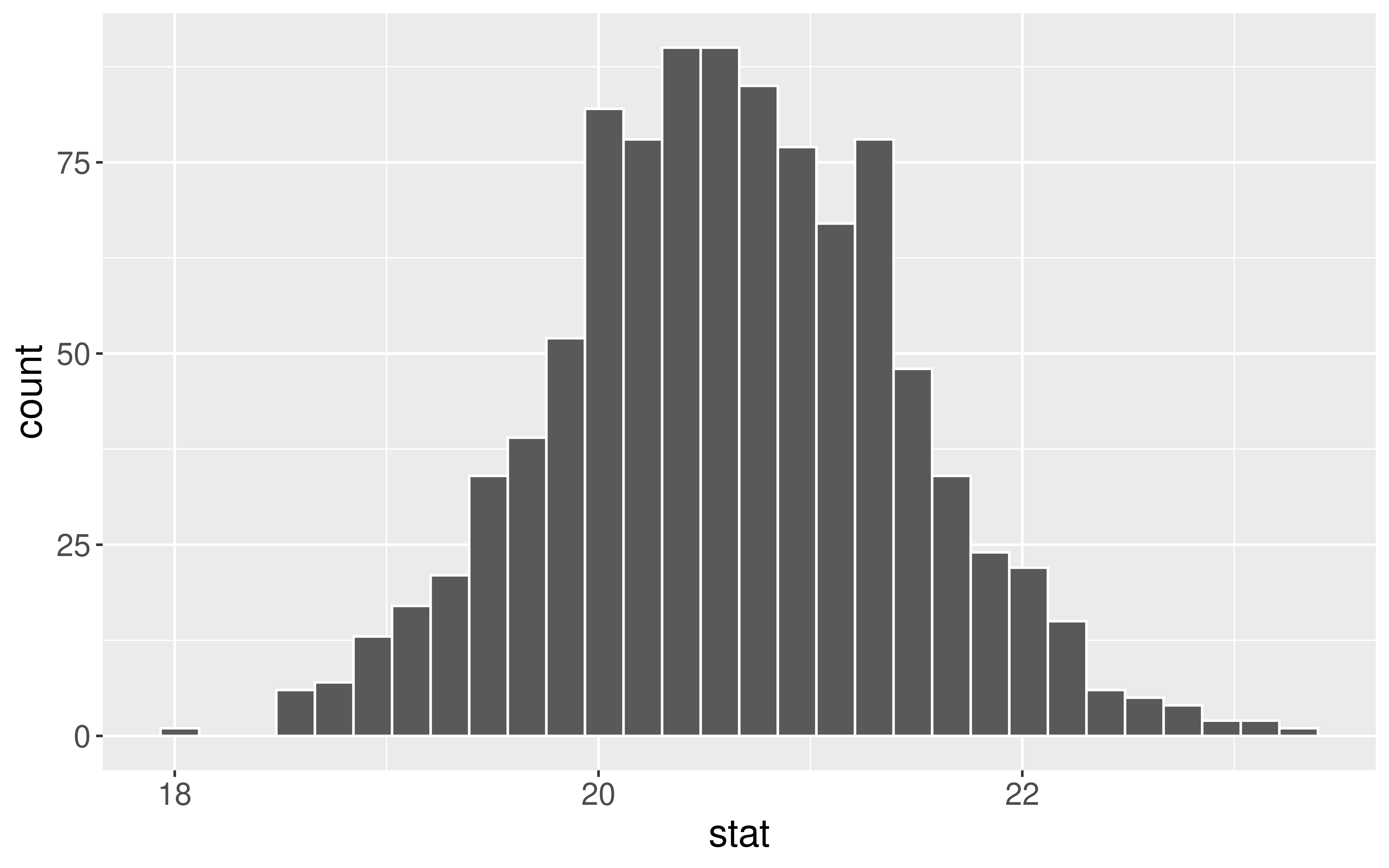

Estimation for a Single Mean – SE Method

# Get confidence interval
ci <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.95,
                          point_estimate = x_bar)
ci
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     19.0     22.2

Interpretation: The point estimate is $ 20.6M. I am 95% confidence that the average amount of money made by all Hollywood movies is between $ 19M and $ 22.2M.

Inline R code: The point estimate is $ 20.6M. I am 95% confidence that the average amount of money made by all Hollywood movies is between $ 19.0243721 M and $ 22.2 M.

Estimation for a Single Mean

# Visualize confidence interval
bootstrap_dist %>%
  visualize() +
  shade_confidence_interval(endpoints = ci)

Estimation for a Single Mean – Percentile Method

# Get confidence interval 
ci_95 <- bootstrap_dist %>% 
  get_confidence_interval(type = "percentile",
                          level = 0.95) 
ci_95
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     19.0     22.3

Estimation for Difference in Means

What is the difference in average amount of money made in the opening weekend between action movies and dramas \((\mu_1 - \mu_2)\)?

# Compute the summary statistic
diff_x_bar <- movies %>%
  drop_na(OpeningWeekend) %>%
  filter(Genre %in% c("Drama", "Action")) %>%
  specify(OpeningWeekend ~ Genre) %>%
  calculate(stat = "diff in means")
diff_x_bar
Response: OpeningWeekend (numeric)
Explanatory: Genre (factor)
# A tibble: 1 × 1
   stat
  <dbl>
1  21.7
  • Why a difference in means?

Estimation for Difference in Means

# Construct bootstrap distribution
bootstrap_dist <- movies %>%
  drop_na(OpeningWeekend) %>%
  filter(Genre %in% c("Drama", "Action")) %>%
  specify(OpeningWeekend ~ Genre) %>%
  generate(reps =  1000, type = "bootstrap") %>%
  calculate(stat = "diff in means",
            order = c("Action", "Drama"))

# Look at bootstrap distribution
ggplot(data = bootstrap_dist,
       mapping = aes(x = stat)) +
  geom_histogram(color = "white")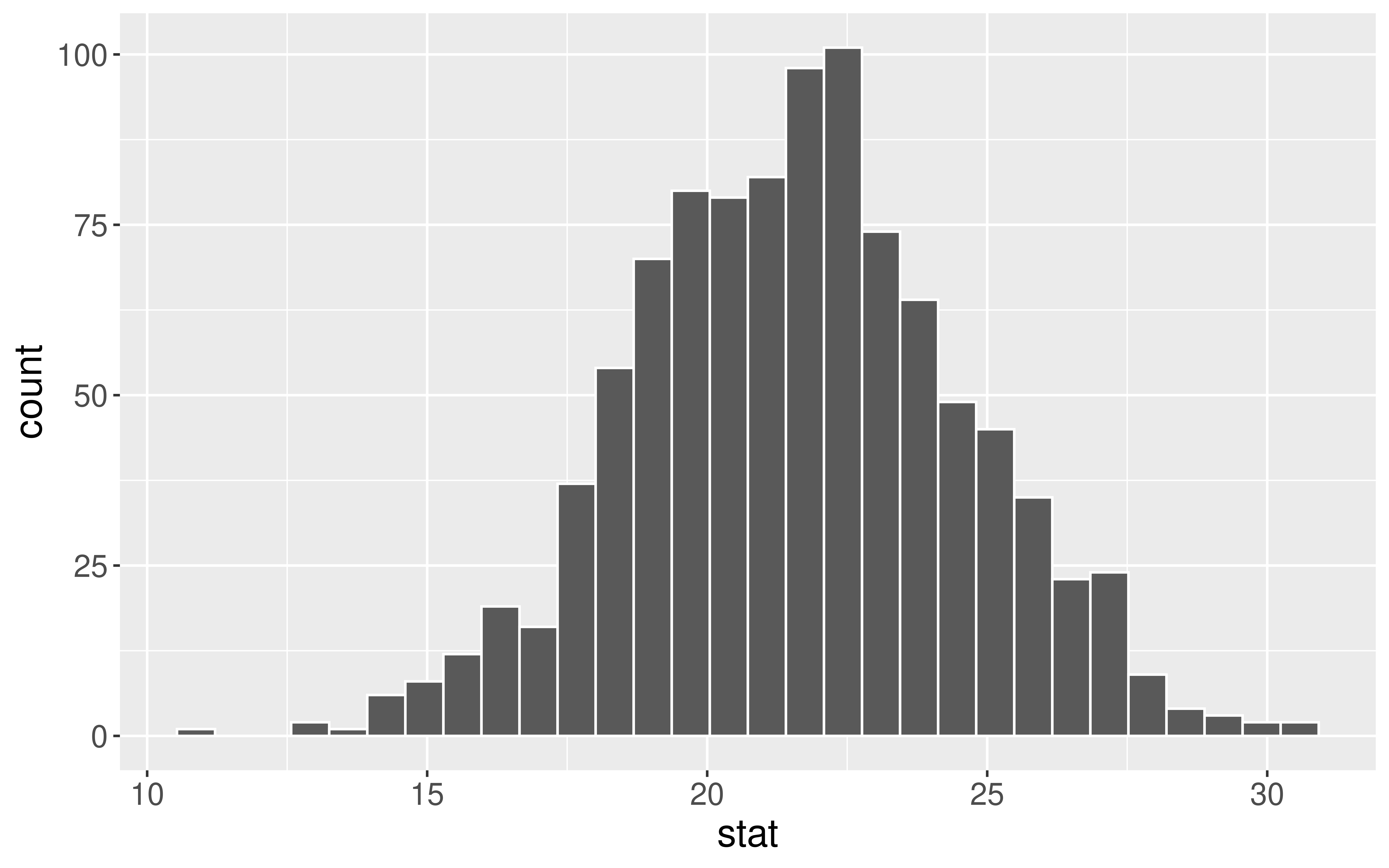

Estimation for Difference in Means – SE Method

# Get confidence interval 
ci_95 <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.95,
                          point_estimate = diff_x_bar) 
ci_95
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     15.9     27.5

Interpretation: The point estimate is $ 21.7M. I am 95% confidence that action movies make, on average, between $ 15.9M and $ 27.5M more than dramas.

Comparing CIs

ci_99 <- bootstrap_dist %>% 
  get_confidence_interval(type = "se", level = 0.99,
                          point_estimate = diff_x_bar)

bootstrap_dist %>%
  visualize() +
  shade_confidence_interval(endpoints = ci_99,
                            fill = "gold1",
                            color = "gold3") +
  shade_confidence_interval(endpoints = ci_95)

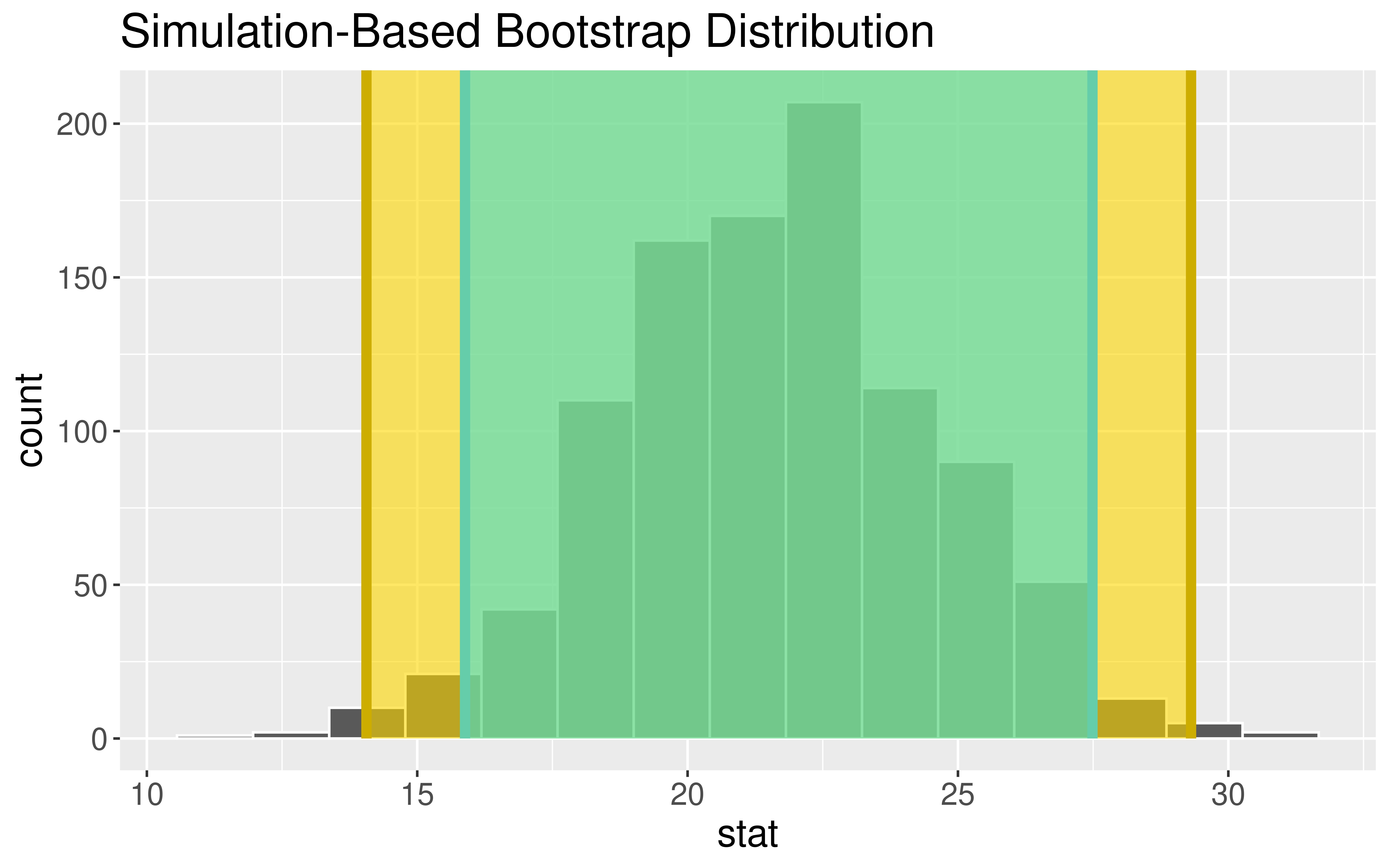
  • Why construct a 95% CI versus a 99% CI?
    • Need to dig into what we mean by confidence!

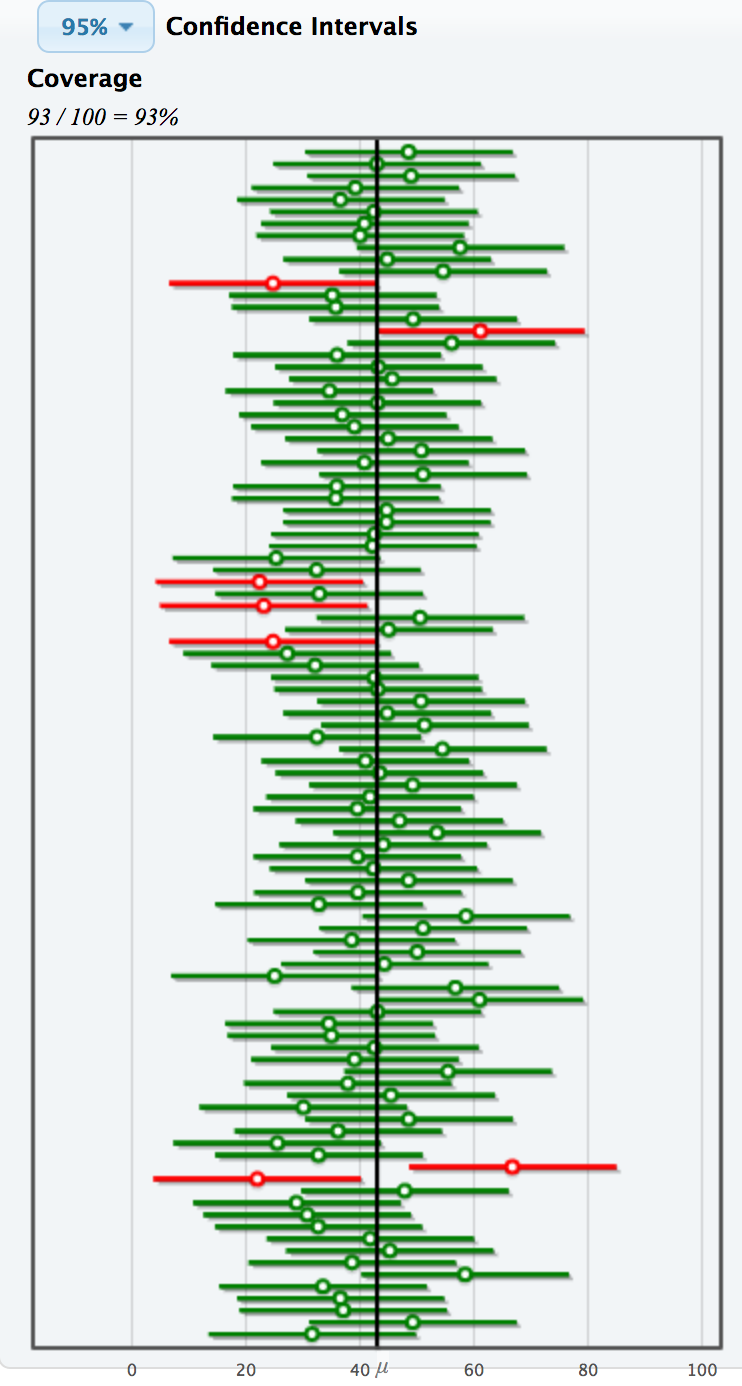
What do we mean by confidence?

  • Confidence level = success rate of the method under repeated sampling

  • How do I know if my ONE CI successfully contains the true value of the parameter?

  • As we increase the confidence level, what happens to the width of the interval?

  • As we increase the sample size, what happens to the width of the interval?

  • As we increase the number of bootstrap samples we take, what happens to the width of the interval?

Interpreting Confidence Intervals

Example: Estimating average household income before taxes in the US

SE Method Formula:

\[ \mbox{statistic} \pm{\mbox{ME}} \]

# A tibble: 1 × 3
     ME  lower  upper
  <dbl>  <dbl>  <dbl>
1 1963. 60517. 64443.

“The margin of [sampling] error can be described as the ‘penalty’ in precision for not talking to everyone in a given population. It describes the range that an answer likely falls between if the survey had reached everyone in a population, instead of just a sample of that population.” – Courtney Kennedy, Director of Survey Research at Pew Research Center

CI = interval of plausible values for the parameter

Safe interpretation: I am P% confident that {insert what the parameter represents in context} is between {insert lower bound} and {insert upper bound}.

Caution: Confidence intervals in the wild

Statement in an article for The BMJ (British Medical Journal):

🤔 The second half of Stat 100 is more conceptually difficult. 🤔

So keep coming to lecture, to section, to wrap-up sessions, and to office hours to get your questions answered!

Reminders:

  • Oct 30th Today: Hex or Treat Day in Stat 100
    • If you are wearing a Halloween costume, come to the front before or after class for your hex sticker or treat!