Decisions, Decisions




Kelly McConville

Stat 100
Week 10 | Fall 2023

Announcements

  • 🎉 We are now accepting Course Assistant/Teaching Fellow applications for Stat 100 for next semester. To apply, fill out this application by Nov 15th.
  • No wrap-up session on Friday due to the university holiday.
  • You are all invited to the Info Session on Data Science Internships: Mon at 4pm in SC 316!

Goals for Today

  • Coding goals (Stat 100 & beyond)
  • Advice on the next stats/coding class
  • Decisions in a hypothesis test
    • Types of errors
  • The power of a hypothesis test

Now that you are at least 25% of the way to a stats secondary, what other classes should you consider?

That Next Stats Class

  • But first… Common Question: How should I describe my post-Stat 100 coding abilities?

  • Potential Answer: You have learned how to write code to analyze data. This includes visualization (ggplot2), data wrangling (dplyr), data importation (readr), modeling, inference (infer) and communication (with Quarto).

  • Follow-up Question: So what coding is there left to learn?

  • Answer: Learning how to program. This includes topics such as control flow, iteration, creating functions, and vectorization.

That Next Coding Class

  • Stat 108: Introduction to Statistical Computing with R
  • CompSci 32: Computational Thinking and Problem Solving
  • CompSci 50: Introduction to Computer Science
  • AP 10: Computing with Python for Scientists and Engineers

That Next Modeling Course

  • Stat 109A: Data Science I & Stat 109B: Data Science II
  • Stat 139: Linear Models
  • Many of the upper-level stats courses are modeling courses (but they do have pre-reqs).

That Next Theory/Methods Course

  • Stat 110: Introduction to Probability
  • Stat 111: Introduction to Statistical Inference

That Next Visualization Course

  • Stat 108: Introduction to Statistical Computing with R
  • CompSci 171: Visualization
  • Stat 106: Data Science for Sports Analytics
    • Not on the books yet but should be coming next academic year.

Another Hypothesis Testing Example

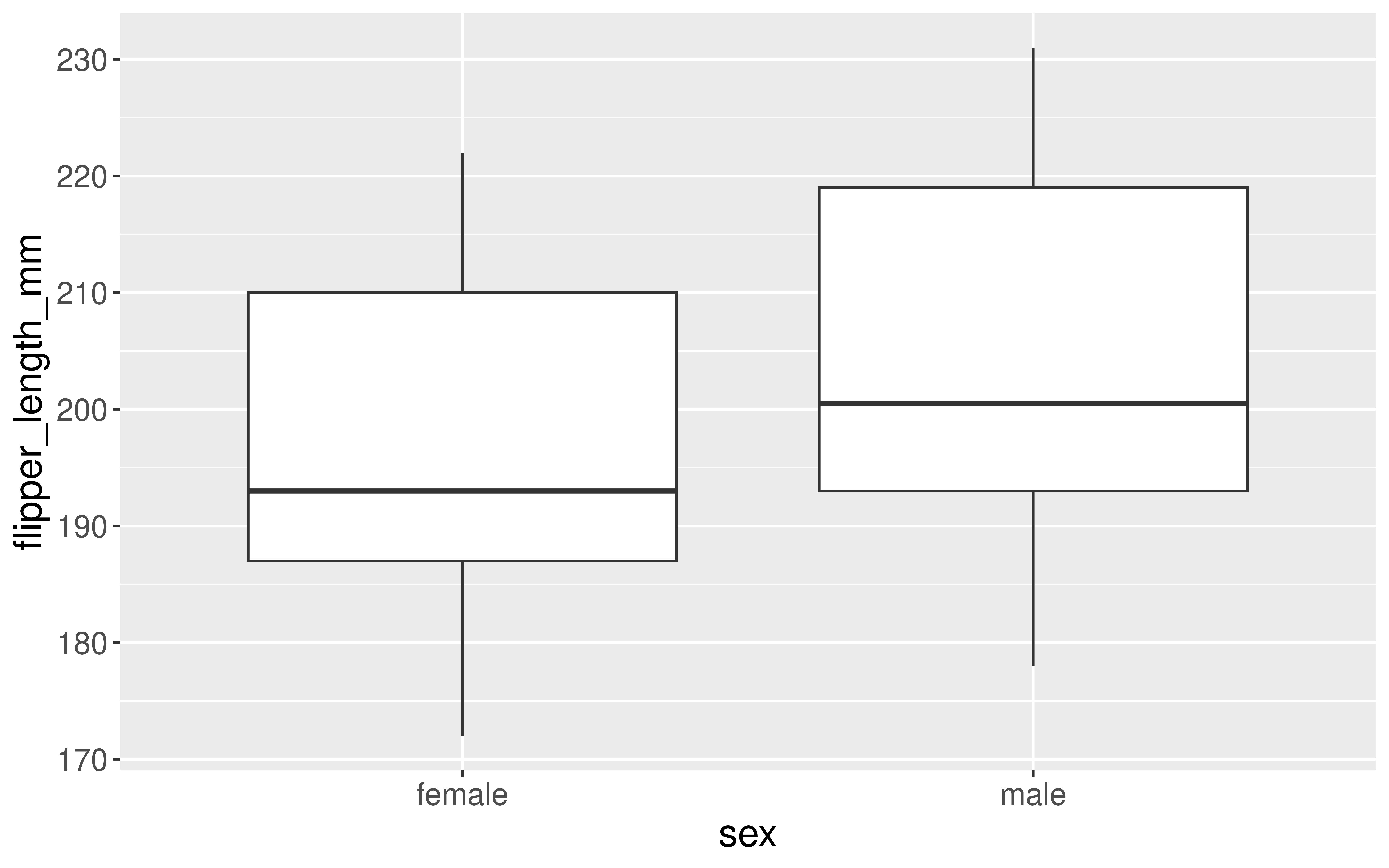
Penguins Example

Let’s return to the penguins data and ask if flipper length varies, on average, by the sex of the penguin.

Research Question: Does flipper length differ by sex?

Response Variable:


Explanatory Variable:


Statistical Hypotheses:

Exploratory Data Analysis

library(infer)
library(tidyverse)
library(palmerpenguins)

penguins %>%
  drop_na(sex) %>%
ggplot(mapping = aes(x = sex,
                     y = flipper_length_mm)) +
  geom_boxplot()

Two-Sided Hypothesis Test

# Compute observed test statistic
test_stat <- penguins %>%
  drop_na(sex) %>%
  specify(flipper_length_mm ~ sex) %>%
  calculate(stat ="diff in means",
            order = c("female", "male"))
test_stat
Response: flipper_length_mm (numeric)
Explanatory: sex (factor)
# A tibble: 1 Ă— 1
   stat
  <dbl>
1 -7.14
# Generate null distribution 
null_dist <- penguins %>%
  drop_na(sex) %>%
  specify(flipper_length_mm ~ sex) %>%
  hypothesize(null = "independence") %>%
  generate(reps = 1000, type = "permute") %>%
  calculate(stat ="diff in means",
            order = c("female", "male"))

Two-Sided Hypothesis Test

# Graph null distribution with test statistic
visualize(null_dist) +
  geom_vline(xintercept = test_stat$stat,
             color = "deeppink", size = 2) +
  geom_vline(xintercept = abs(test_stat$stat),
             color = "deeppink", size = 2)

Two-Sided Hypothesis Test

# Compute p-value
p_value <- null_dist %>%
  get_p_value(obs_stat = test_stat,
              direction = "two_sided")
p_value
# A tibble: 1 Ă— 1
  p_value
    <dbl>
1       0

Interpretation of \(p\)-value: If the mean flipper length does not differ by sex in the population, the probability of observing a difference in the sample means of at least 7.142316 mm (in magnitude) is equal to 0.

Conclusion: These data represent evidence that flipper length does vary by sex.

Hypothesis Testing: Decisions, Decisions

Once you get to the end of a hypothesis test you make one of two decisions:

  • P-value is small.
    • I have evidence for \(H_a\). Reject \(H_o\).
  • P-value is not small.
    • I don’t have evidence for \(H_a\). Fail to reject \(H_o\).

Sometimes we make the correct decision. Sometimes we make a mistake.

Hypothesis Testing: Decisions, Decisions

Let’s create a table of potential outcomes.












\(\alpha\) = prob of Type I error under repeated sampling = prob reject \(H_o\) when it is true

\(\beta\) = prob of Type II error under repeated sampling = prob fail to reject \(H_o\) when \(H_a\) is true.

Hypothesis Testing: Decisions, Decisions

Typically set \(\alpha\) level beforehand.

Use \(\alpha\) to determine “small” for a p-value.

  • P-value is small \(< \alpha\).
    • I have evidence for \(H_a\). Reject \(H_o\).
  • P-value is not small \(\geq \alpha\).
    • I don’t have evidence for \(H_a\). Fail to reject \(H_o\).

Hypothesis Testing: Decisions, Decisions

Question: How do I select \(\alpha\)?

  • Will depend on the convention in your field.

  • Want a small \(\alpha\) and a small \(\beta\). But they are related.

    • The smaller \(\alpha\) is the larger \(\beta\) will be.

  • Choose a lower \(\alpha\) (e.g., 0.01, 0.001) when the Type I error is worse and a higher \(\alpha\) (e.g., 0.1) when the Type II error is worse.

  • Can’t easily compute \(\beta\). Why?

  • One more important term:

    • Power = probability reject \(H_o\) when the alternative is true.

Example

Suppose we have a baseball player who has been a 0.250 career hitter who suddenly improves to be a 0.333 hitter. He wants a raise but needs to convince his manager that he has genuinely improved. The manager offers to examine his performance in 20 at-bats.

Ho:

Ha:

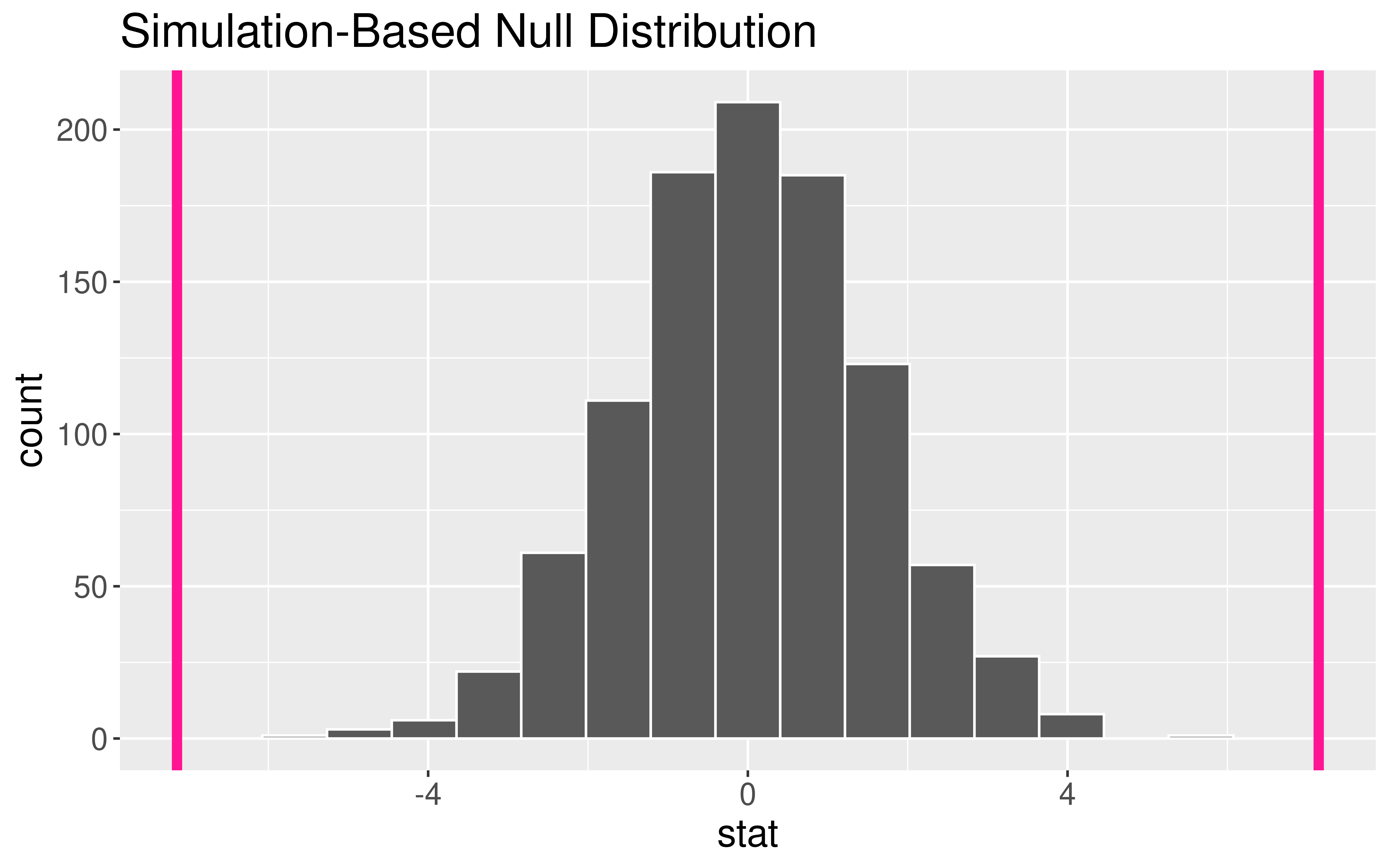
  • When \(\alpha\) is set to \(0.05\), he needs to hit 9 or more to get a small enough p-value to reject \(H_o\).

  • When \(\alpha\) is set to \(0.05\), the power of this test is 0.204.

  • Why is the power so low?

  • What aspects of the test could the baseball player change to increase the power of the test?

Example

Suppose we have a baseball player who has been a 0.250 career hitter who suddenly improves to be a 0.333 hitter. He wants a raise but needs to convince his manager that he has genuinely improved. The manager offers to examine his performance in 20 100 at-bats.

What will happen to the power of the test if we increase the sample size?

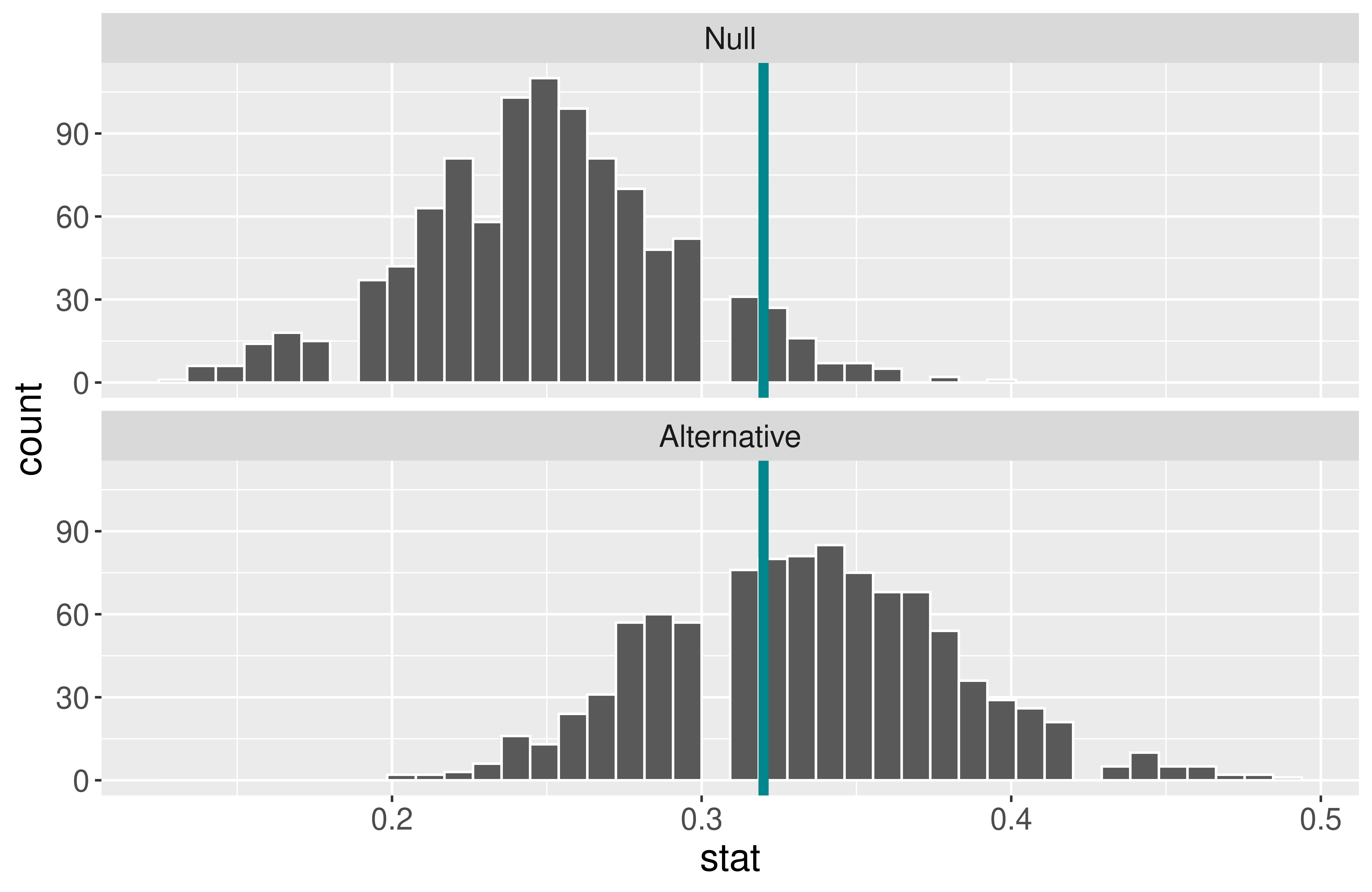
  • Increasing the sample size increases the power.

  • When \(\alpha\) is set to \(0.05\) and the sample size is now 100, the power of this test is 0.57.

Example

Suppose we have a baseball player who has been a 0.250 career hitter who suddenly improves to be a 0.333 hitter. He wants a raise but needs to convince his manager that he has genuinely improved. The manager offers to examine his performance in 20 100 at-bats.

What will happen to the power of the test if we increase \(\alpha\) to 0.1?

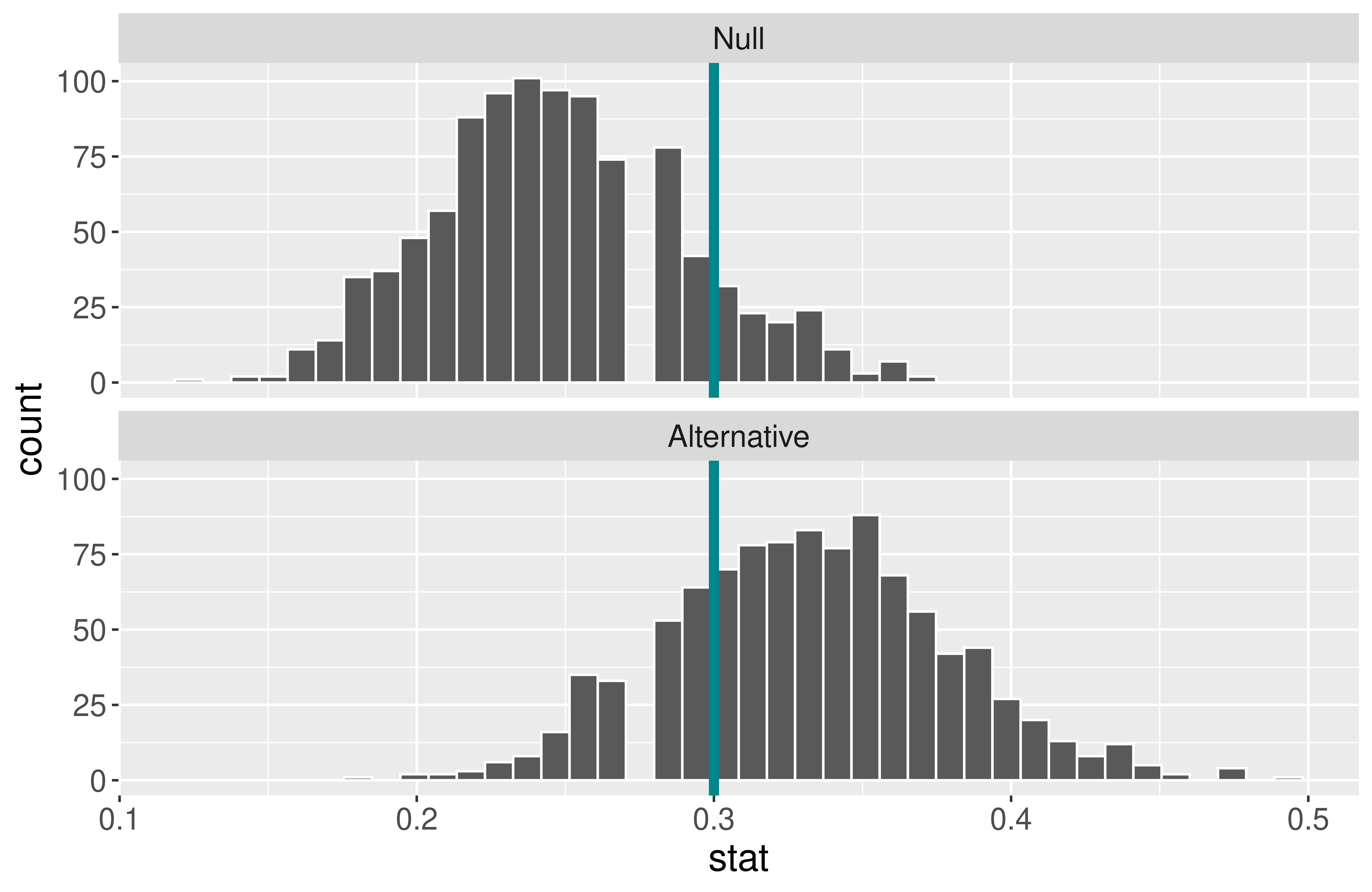
  • Increasing \(\alpha\) increases the power.
    • Decreases \(\beta\).
  • When \(\alpha\) is set to \(0.1\) and the sample size is 100, the power of this test is 0.71.

Example

Suppose we have a baseball player who has been a 0.250 career hitter who suddenly improves to be a 0.333 0.400 hitter. He wants a raise but needs to convince his manager that he has genuinely improved. The manager offers to examine his performance in 20 100 at-bats.

What will happen to the power of the test if he is an even better player?

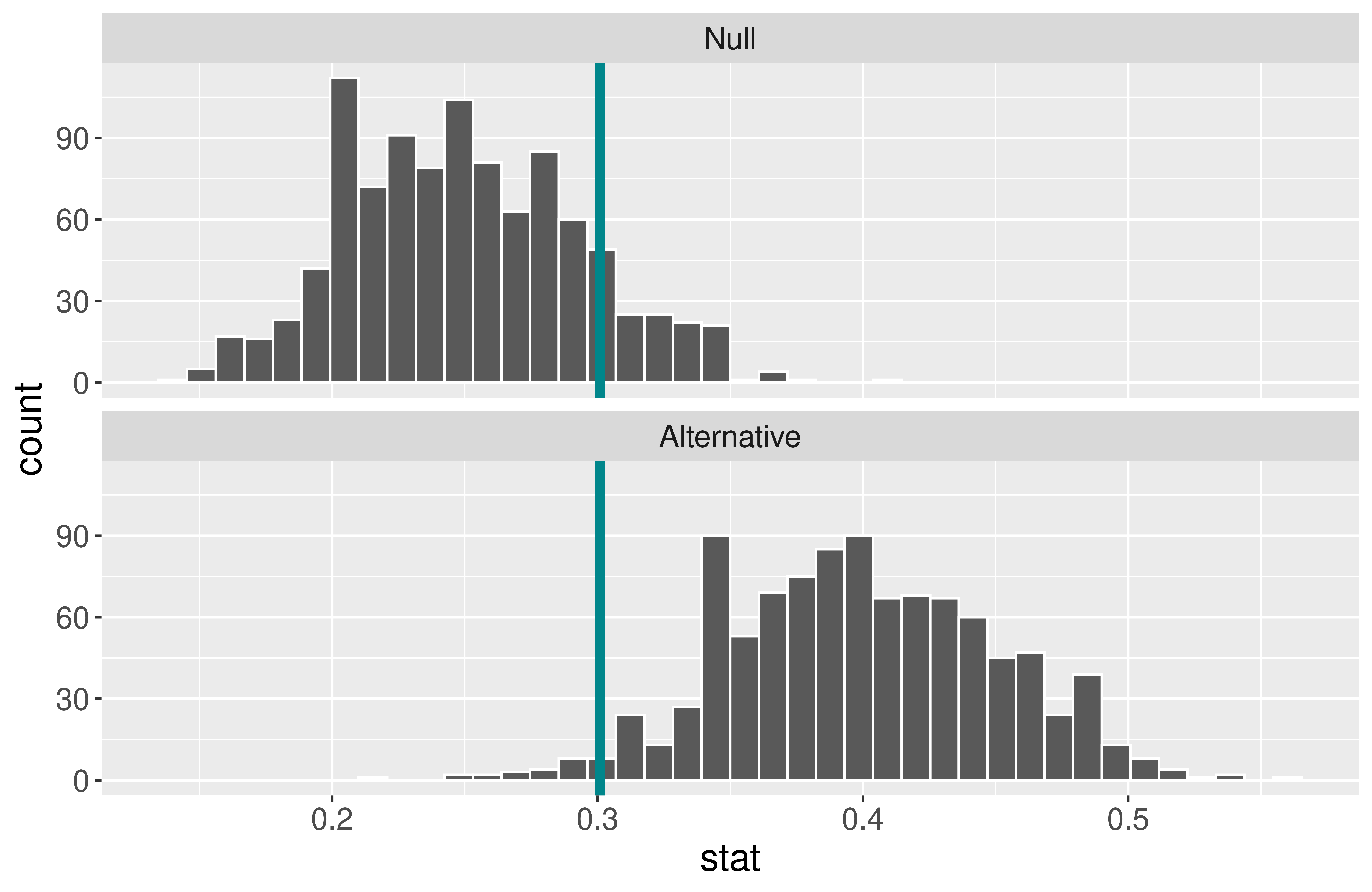
  • Effect size: Difference between true value of the parameter and null value.

    • Often standardized.

  • Increasing the effect size increases the power.

  • When \(\alpha\) is set to \(0.1\), the sample size is 100, and the true probability of hitting the ball is 0.4, the power of this test is 0.97.

Computing Power

  1. Generate a null distribution:
# Create a dummy dataset with the correct sample size
dat <- data.frame(at_bats = c(rep("hit", 80), 
                              rep("miss", 20)))


null <- dat %>%
  specify(response = at_bats, success = "hit") %>%
  hypothesize(null = "point", p = 0.25) %>%
  generate(reps = 1000, type = "draw") %>%
  calculate(stat = "prop")

ggplot(data = null, mapping = aes(x = stat)) +
  geom_histogram(bins = 27, color = "white")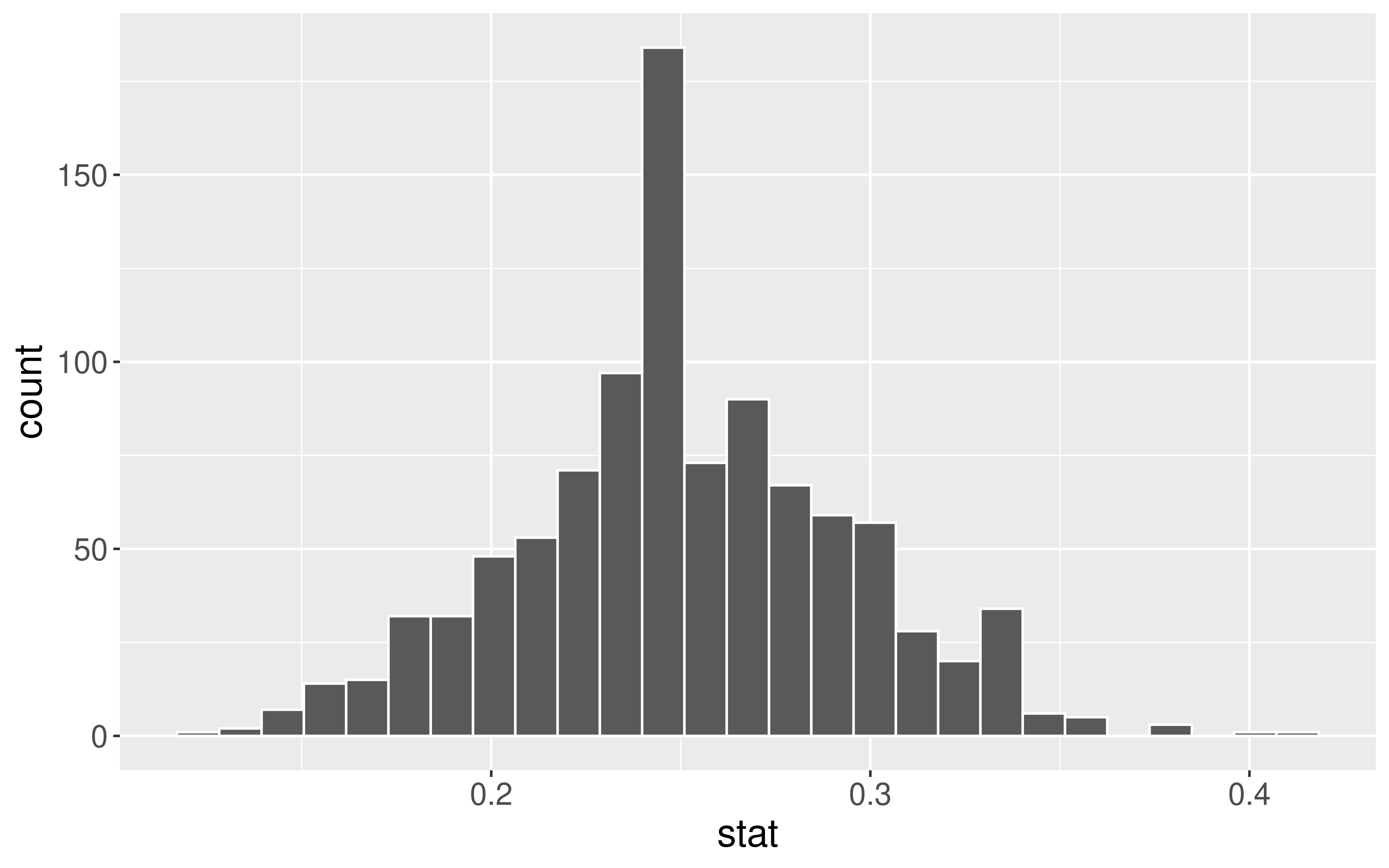

Computing Power

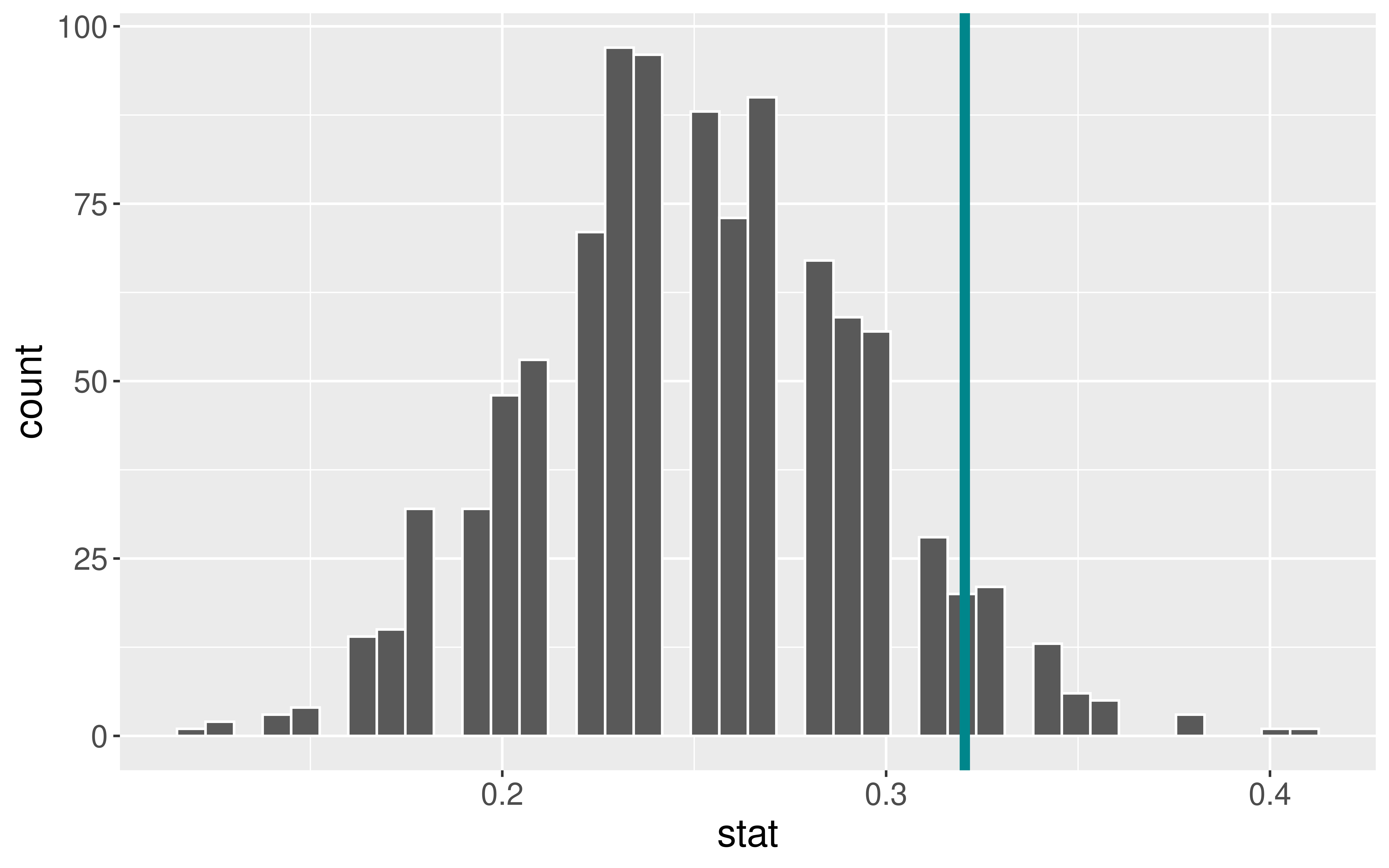
  1. Determine the “critical value(s)” where \(\alpha = 0.05\)
quantile(null$stat, 0.95)
   95% 
0.3205 
ggplot(data = null, mapping = aes(x = stat)) +
  geom_histogram(bins = 40, color = "white") +
  geom_vline(xintercept = quantile(null$stat, 0.95),
             size = 2,
             color = "turquoise4")

Computing Power

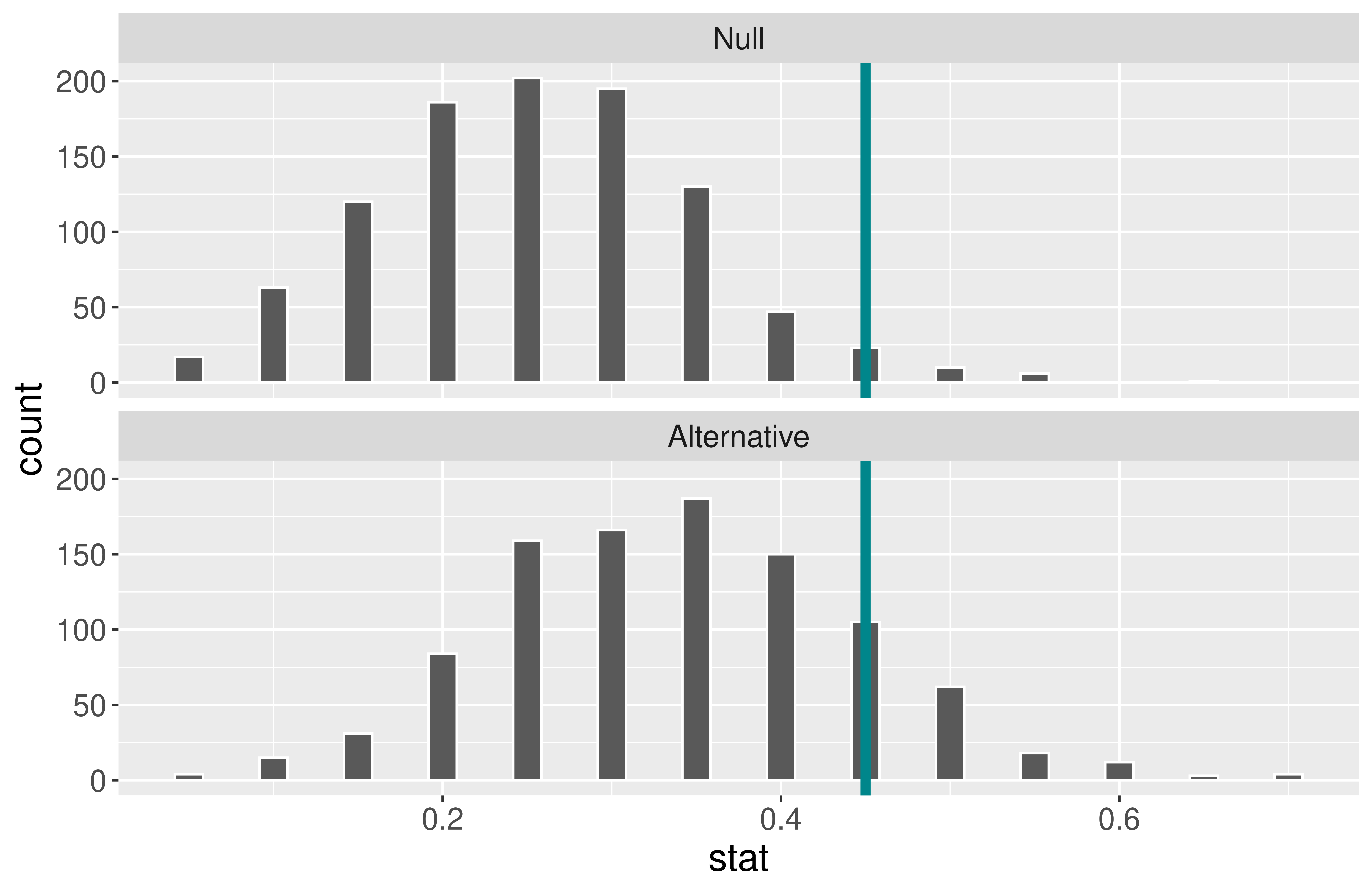
  1. Construct the alternative distribution.
alt <- dat %>%
  specify(response = at_bats, success = "hit") %>%
  hypothesize(null = "point", p = 0.333) %>%
  generate(reps = 1000, type = "draw") %>%
  calculate(stat = "prop") %>%
  mutate(dist = "Alternative")

ggplot(data = alt, mapping = aes(x = stat)) +
  geom_histogram(bins = 27, color = "white") +
  geom_vline(xintercept = quantile(null$stat, 0.95),
             size = 2,
             color = "turquoise4")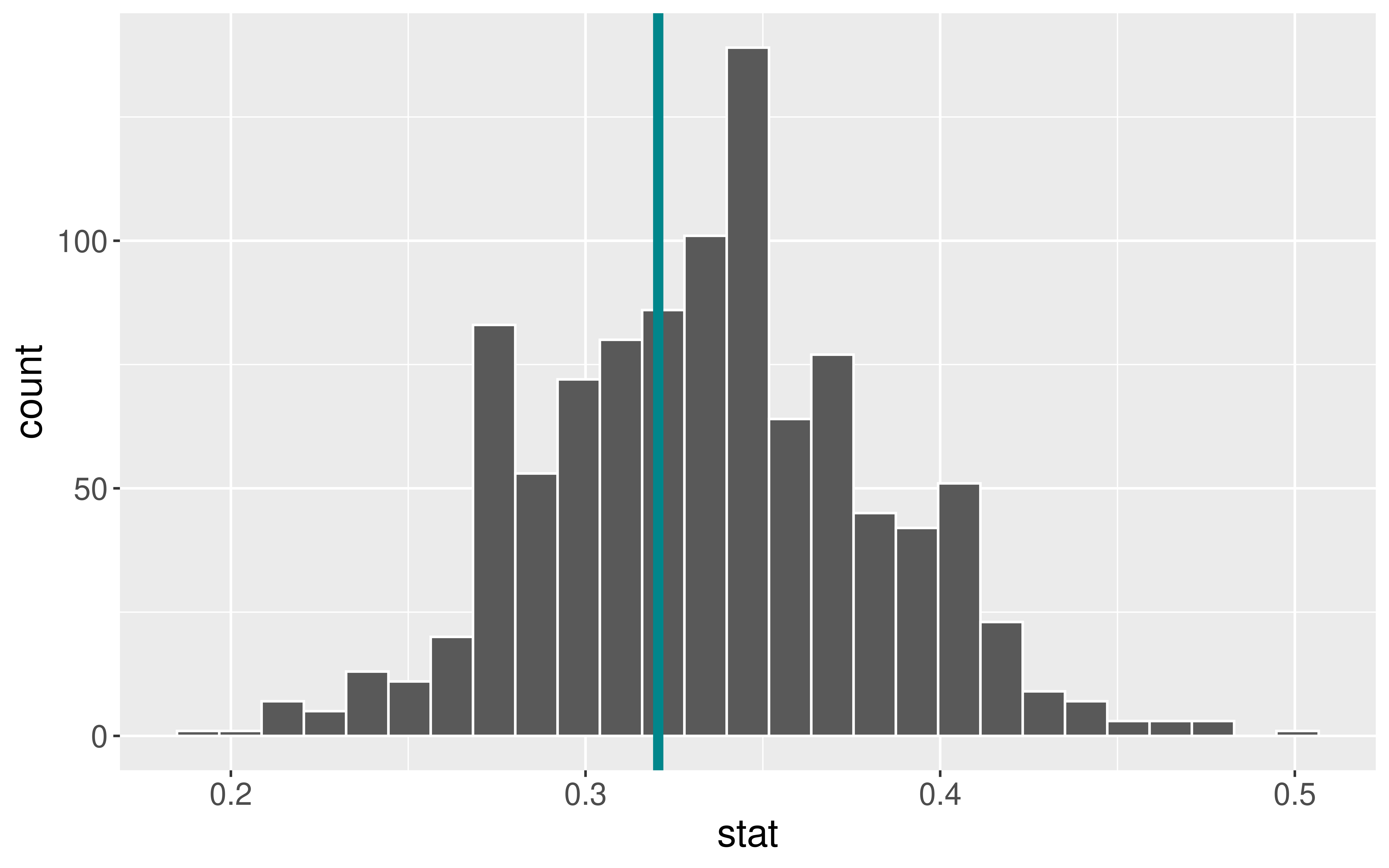

Computing Power

  1. Find the probability of the critical value or more extreme under the alternative distribution.
alt %>%
  summarize(power = mean(stat > quantile(null$stat, 0.95)))
# A tibble: 1 Ă— 1
  power
  <dbl>
1 0.568

Thoughts on Power

  • What aspects of the test did the player actually have control over?

  • Why is it easier to set \(\alpha\) than to set \(\beta\) or power?

  • Considering power before collecting data is very important!

  • The danger of under-powered studies

    • EX: Turning right at a red light

Reporting Results in Journal Articles

Reminders:

  • 🎉 We are now accepting Course Assistant/Teaching Fellow applications for Stat 100 for next semester. To apply, fill out this application by Nov 15th.
    • About 10-12 hours of work per week.
    • Primary responsibilities: Attend weekly team meetings, lead a discussion section, hold office hours, grade assessments.